题目内容

12．已知sinα=$\frac{2\sqrt{5}}{5}$，α∈（0，$\frac{π}{2}$），则tan2α=（　　）
A．-$\frac{4}{3}$B．$\frac{4}{3}$C．-$\frac{1}{2}$D．2

分析 由同角三角函数间的基本关系先求cosα，tanα的值，由二倍角的正切函数公式即可求值．

解答 解：∵sinα=$\frac{2\sqrt{5}}{5}$，α∈（0，$\frac{π}{2}$），
∴cosα=$\sqrt{1-si{n}^{2}α}$=$\frac{\sqrt{5}}{5}$，tanα=$\frac{sinα}{cosα}$=2，
∴tan2α=$\frac{2tanα}{1-ta{n}^{2}α}$=$\frac{4}{1-4}$=-$\frac{4}{3}$．
故选：A．

点评 本题主要考查了同角三角函数间的基本关系，二倍角的正切函数公式的应用，属于基础题．

练习册系列答案
相关题目
2．已知复数z=$\frac{2i}{1-i}$-1，其中i为虚数单位，则z的模为$\sqrt{5}$．
3．已知等比数列{an}的前n项和Sn，且a1+a3=$\frac{5}{2}$，a2+a4=$\frac{5}{4}$，则$\frac{S_n}{a_n}$=（　　）
A．4n-1B．4n-1C．2n-1D．2n-1
20．设命题p：函数f（x）=ex-1在R上为增函数；命题q：函数f（x）=cos2x为奇函数．则下列命题中真命题是（　　）
A．p∧qB．（￢p）∨qC．（￢p）∧（￢q）D．p∧（￢q）
7．如图，正方形ABCD的边长为2，O为AD的中点，射线OP从OA出发，绕着点O顺时针方向旋转至OD，在旋转的过程中，记∠AOP为x（x∈[0，π]），OP所经过的在正方形ABCD内的区域（阴影部分）的面积S=f（x），那么对于函数f（x）有以下三个结论：
①f（$\frac{π}{3}$）=$\frac{\sqrt{3}}{2}$；
②函数f（x）在区间$（\frac{π}{2}，π）$上为减函数；
③任意$x∈[0，\frac{π}{2}]$，都有f（x）+f（π-x）=4．
其中所有正确结论的序号是①③．
17．复数z=i（1+2i）（i为虚数单位），则$\overline{z}$=-2-i．
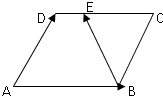4．在边长为1的菱形ABCD中，∠A=60°，E是线段CD上一点，满足|$\overrightarrow{CE}$|=2||$\overrightarrow{DE}$|，如图所示，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$．
（1）用$\overrightarrow{a}$，$\overrightarrow{b}$表示$\overrightarrow{BE}$；
（2）在线段BC上是否存在一点F满足AF⊥BE？若存在，确定F点的位置，并求|$\overrightarrow{AF}$|；若不存在，请说明理由．
1．已知函数f（x）=lnx-$\frac{1}{2}$ax2+x，a∈R．
（Ⅰ）若f（1）=0，求函数f（x）的最大值；
（Ⅱ）令g（x）=f（x）-（ax-1），求函数g（x）的单调区间；
（Ⅲ）若a=-2，正实数x1，x2满足f（x1）+f（x2）+x1x2=0，证明x1+x2≥$\frac{\sqrt{5}-1}{2}$．
1．在三维空间直角坐标系中，对其中任何一向量$\overrightarrow{x}$=（x1，x2，x3），定义范数||x||，它满足以下性质：
①||x||≥0，当且仅当x为零向量时，不等式取等号；
②对任意实数λ，||λx||=|λ|•||x||（注：此处点乘号为普通的乘号，无点乘意义）；
③||x||+||y||≥||x+y||．
试求解以下问题：
在二维平面直角坐标系中，有向量$\overrightarrow{x}$=（x1，x2），下面给出的几个表达式中，可能表示向量$\overrightarrow{x}$的范数是②⑤（把所有正确的答案的序号都填上）．
①$\sqrt{{{x}_{1}}^{2}}$+2x22；
②$\sqrt{{{x}_{1}}^{2}+2{{x}_{2}}^{2}}$；
③$\sqrt{2{{x}_{1}}^{2}-{{x}_{2}}^{2}}$；
④$\sqrt{{{x}_{1}}^{2}+{{x}_{2}}^{2}+2}$；
⑤$\sqrt{{{x}_{1}}^{2}+{{x}_{2}}^{2}}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网