题目内容
已知:函数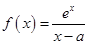 (其中常数
(其中常数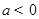 ).
).
(Ⅰ)求函数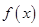 的定义域及单调区间;
的定义域及单调区间;
(Ⅱ)若存在实数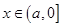 ,使得不等式
,使得不等式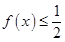 成立,求a的取值范围
成立,求a的取值范围
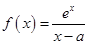 (其中常数
(其中常数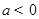 ).
).(Ⅰ)求函数
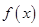 的定义域及单调区间;
的定义域及单调区间;(Ⅱ)若存在实数
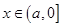 ,使得不等式
,使得不等式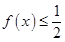 成立,求a的取值范围
成立,求a的取值范围(Ⅰ)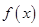 的单调递增区间为
的单调递增区间为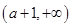 ,单调递减区间为
,单调递减区间为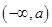 ,
,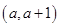
(Ⅱ)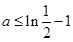
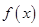 的单调递增区间为
的单调递增区间为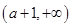 ,单调递减区间为
,单调递减区间为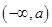 ,
,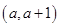
(Ⅱ)
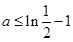
本试题主要是考查导数在研究函数中的运用。求解函数的最值以及函数的定义域和单调性的综合运用。
(1)因为函数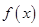 的定义域为
的定义域为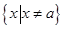 .
.
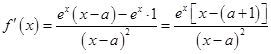 结合导数的正负来得到单调性的判定。
结合导数的正负来得到单调性的判定。
(2)由题意可知,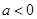 ,且
,且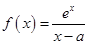 在
在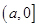 上的最小值小于等于
上的最小值小于等于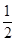 时,存在实数
时,存在实数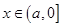 ,使得不等式
,使得不等式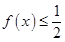 成立,那么对于参数a分类讨论得到结论。
成立,那么对于参数a分类讨论得到结论。
解:(Ⅰ)函数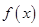 的定义域为
的定义域为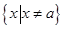 .
.
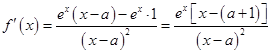 . 由
. 由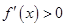 ,解得
,解得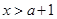 . 由
. 由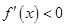 ,解得
,解得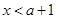 且
且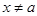 .∴
.∴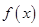 的单调递增区间为
的单调递增区间为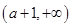 ,单调递减区间为
,单调递减区间为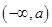 ,
,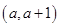 .
.
(Ⅱ)由题意可知,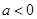 ,且
,且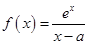 在
在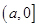 上的最小值小于等于
上的最小值小于等于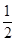 时,存在实数
时,存在实数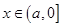 ,使得不等式
,使得不等式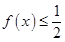 成立.
成立.
若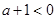 即
即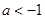 时,
时,
∴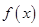 在
在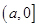 上的最小值为
上的最小值为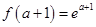 .
.
则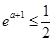 ,得
,得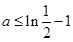 .
.
若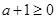 即
即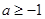 时,
时,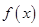 在
在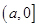 上单调递减,则
上单调递减,则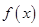 在
在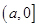 上的最小值为
上的最小值为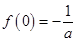 .
.
由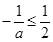 得
得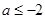 (舍).
(舍).
综上所述,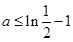 .
.
(1)因为函数
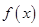 的定义域为
的定义域为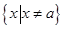 .
. 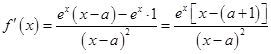 结合导数的正负来得到单调性的判定。
结合导数的正负来得到单调性的判定。(2)由题意可知,
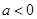 ,且
,且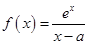 在
在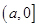 上的最小值小于等于
上的最小值小于等于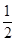 时,存在实数
时,存在实数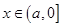 ,使得不等式
,使得不等式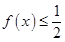 成立,那么对于参数a分类讨论得到结论。
成立,那么对于参数a分类讨论得到结论。解:(Ⅰ)函数
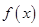 的定义域为
的定义域为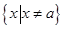 .
. 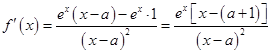 . 由
. 由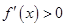 ,解得
,解得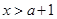 . 由
. 由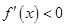 ,解得
,解得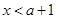 且
且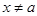 .∴
.∴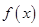 的单调递增区间为
的单调递增区间为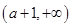 ,单调递减区间为
,单调递减区间为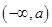 ,
,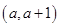 .
. (Ⅱ)由题意可知,
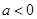 ,且
,且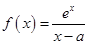 在
在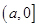 上的最小值小于等于
上的最小值小于等于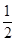 时,存在实数
时,存在实数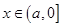 ,使得不等式
,使得不等式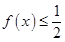 成立.
成立. 若
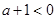 即
即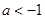 时,
时,| x | 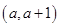 | a+1 | 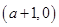 |
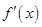 | - | 0 | + |
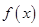 | ↘ | 极小值 | ↗ |
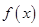 在
在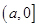 上的最小值为
上的最小值为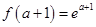 .
.则
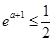 ,得
,得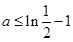 .
. 若
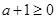 即
即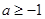 时,
时,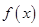 在
在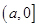 上单调递减,则
上单调递减,则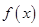 在
在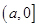 上的最小值为
上的最小值为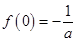 .
.由
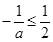 得
得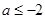 (舍).
(舍).综上所述,
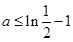 .
. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
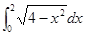 的结果是( )
的结果是( )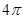
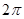
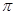
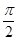
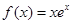 .
.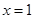 处的切线方程.
处的切线方程.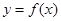 的导函数
的导函数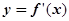 的图象,给出下列命题:
的图象,给出下列命题: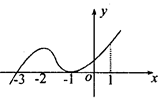

 的极大值等于 .
的极大值等于 .
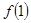 )的切线方程
)的切线方程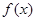 的极值
的极值 ,如果存在曲线上的点
,如果存在曲线上的点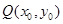 ,且
,且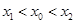 ,使得曲线在点
,使得曲线在点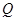 处的切线
处的切线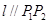 ,则称
,则称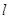 为弦
为弦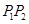 的陪伴切线.
的陪伴切线.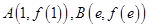 ,试求弦
,试求弦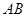 的陪伴切线
的陪伴切线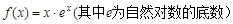
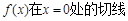 方程;
方程;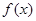 的单调区间.
的单调区间.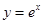 在点
在点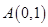 处的切线斜率为
处的切线斜率为