题目内容
6.已知$\overrightarrow{a}$=(1,-2),$\overrightarrow{b}$=(4,2)则2$\overrightarrow{a}$与($\overrightarrow{a}-\overrightarrow{b}$)的夹角为θ,则cosθ=$\frac{\sqrt{5}}{5}$.分析 利用向量的数量积运算和夹角公式即可得出.
解答 解:∵$\overrightarrow{a}$=(1,-2),$\overrightarrow{b}$=(4,2),则2$\overrightarrow{a}$=(2,-4)与$\overrightarrow{a}-\overrightarrow{b}$=(-3,-4),
∴cosθ=$\frac{2\overrightarrow{a}•(\overrightarrow{a}-\overrightarrow{b})}{\left|2\overrightarrow{a}\right||\overrightarrow{a}-\overrightarrow{b}|}$=$\frac{-6+16}{\sqrt{4+16}×\sqrt{9+16}}$=$\frac{\sqrt{5}}{5}$.
故答案为:$\frac{\sqrt{5}}{5}$.
点评 本题考查了向量的数量积运算和夹角公式,属于中档题.

练习册系列答案
相关题目
16.若函数f(x)=$\left\{\begin{array}{l}{{x}^{3}-2x+{a}^{2},x≤1}\\{\frac{15a}{3x+1},x>1}\end{array}\right.$在点x=1处连续,则实数a等于( )
| A. | 4 | B. | -$\frac{1}{4}$ | C. | -$\frac{1}{4}$或-4 | D. | -$\frac{1}{4}$或4 |
1.在(x2+x-y)3的展开式中,x3y的系数等于( )
| A. | -6 | B. | 6 | C. | -3 | D. | 3 |
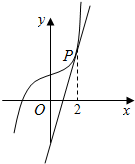 如图,已知函数f(x)=ax3+b,其图象上一点P处的切线为 l:y=4x-4,且点P的横坐标为2.
如图,已知函数f(x)=ax3+b,其图象上一点P处的切线为 l:y=4x-4,且点P的横坐标为2.