题目内容
【题目】给出下列命题:
①若![]() ,
, ![]() 是第一象限角且
是第一象限角且![]() ,则
,则![]() ;
;
②函数![]() 在
在![]() 上是减函数;
上是减函数;
③![]() 是函数
是函数![]() 的一条对称轴;
的一条对称轴;
④函数![]() 的图象关于点
的图象关于点![]() 成中心对称;
成中心对称;
⑤设![]() ,则函数
,则函数![]() 的最小值是
的最小值是![]() ,其中正确命题的序号为 __________.
,其中正确命题的序号为 __________.
【答案】③⑤
【解析】对于①,![]() 时,
时, ![]() ,而
,而![]() ,故①错误;对于②,
,故①错误;对于②,![]() 在
在![]() 上递增,故②错误;对于③,
上递增,故②错误;对于③,![]() 时,
时, ![]() ,
, ![]() 是
是![]() 的对称轴,故③正确;对于④,
的对称轴,故③正确;对于④,![]() 时,
时, ![]() 不是
不是![]() 的对称中心,故④错误;对于⑤,
的对称中心,故④错误;对于⑤,![]() ,设
,设![]() 因为
因为![]() ,所以
,所以![]() ,则
,则![]() ,
, ![]() 在
在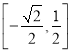 上递增,在
上递增,在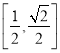 上递减,因为
上递减,因为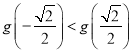 可得
可得![]() 时,
时, ![]() ,即函数
,即函数![]() 的最小值是
的最小值是![]() ,故⑤正确,故答案为③⑤.
,故⑤正确,故答案为③⑤.
【 方法点睛】本题主要通过对多个命题真假的判断,综合考查三角函数的单调性、三角函数的奇偶性、三角函数的图象与性质,属于难题.这种题型综合性较强,也是高考的命题热点,同学们往往因为某一处知识点掌握不好而导致“全盘皆输”,因此做这类题目更要细心、多读题,尽量挖掘出题目中的隐含条件,另外,要注意从简单的自己已经掌握的知识点入手,然后集中精力突破较难的命题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
