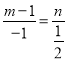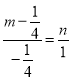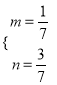题目内容
【题目】已知函数f(x)=alnx+ ![]() ,a∈R.
,a∈R.
(1)若f(x)的最小值为0,求实数a的值;
(2)证明:当a=2时,不等式f(x)≥ ![]() ﹣e1﹣x恒成立.
﹣e1﹣x恒成立.
【答案】
(1)解:∵f(x)=alnx+ ![]() =alnx+
=alnx+ ![]() ,
,
∴f′(x)= ![]() (x>0).
(x>0).
当a≤0时,f′(x)<0,f(x)在(0,+∞)上是减函数,f(x)的最小值不为0;
当a>0时,f′(x)= ![]() =
= ![]() .
.
当x∈(0, ![]() )时,f′(x)<0;当x∈(
)时,f′(x)<0;当x∈( ![]() ,+∞)时,f′(x)>0.
,+∞)时,f′(x)>0.
∴f(x)在(0, ![]() )上为减函数,在(
)上为减函数,在( ![]() ,+∞)上为增函数,
,+∞)上为增函数,
∴ ![]() =
= ![]() ,
,
令g(a)= ![]() ,则g′(a)=
,则g′(a)= ![]() (a>0).
(a>0).
当a∈(0,2)时,g′(a)>0;当a∈(2,+∞)时,g′(a)<0,
∴g(a)在(0,2)上为增函数,在(2,+∞)上为减函数,则g(a)max=g(2)=0.
∴f(x)的最小值为0,实数a的值为2
(2)证明:当a=2时,f(x)=2lnx+ ![]() ,x>1,
,x>1,
令h(x)=f(x)﹣ ![]() +e1﹣x=2lnx+
+e1﹣x=2lnx+ ![]()
![]() ,
,
则h′(x)= ![]() =
= ![]() ,
,
记q(x)=2x2+x﹣2﹣x3e1﹣x,则q′(x)=4x+1+x2(x﹣3)e1﹣x,
∵x>1,0<e1﹣x<1,
∴当1<x<3时,q′(x)>4x+1+x2(x﹣3)=x3﹣3x2+4x+1>0,
又∵当x≥3时,q′(x)=4x+1+x2(x﹣3)e1﹣x>0,
∴当x>1时,q′(x)=4x+1+x2(x﹣3)e1﹣x>0恒成立,
∴q(x)在(1,+∞)上单调递增,q(x)>q(1)=2+1﹣2﹣1=0,
∴h′(x)>0恒成立,h(x)在(1,+∞)上单调递增,
∴h(x)>h(1)=0+1﹣1﹣1+1=0,即当a=2时,不等式f(x)≥ ![]() ﹣e1﹣x恒成立.
﹣e1﹣x恒成立.
【解析】(1)求出原函数的导函数,对a分类分析,可知当a≤0时,f′(x)<0,f(x)在(0,+∞)上是减函数,f(x)的最小值不为0;当a>0时,求出导函数的零点,可得原函数的单调性,求其最小值,由最小值为0进一步利用导数求得a值;(2)通过构造函数h(x)=2lnx+ ![]()
![]() ,问题转化为证明h′(x)>0恒成立,进而再次构造函数,二次求导,整理即得结论.
,问题转化为证明h′(x)>0恒成立,进而再次构造函数,二次求导,整理即得结论.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】北京时间3月10日,CBA半决赛开打,采用7局4胜制(若某对取胜四场,则终止本次比赛,并获得进入决赛资格),采用2﹣3﹣2的赛程,辽宁男篮将与新疆男篮争夺一个决赛名额,由于新疆队常规赛占优,决赛时拥有主场优势(新疆先两个主场,然后三个客场,再两个主场),以下是总决赛赛程:
日期 | 比赛队 | 主场 | 客场 | 比赛时间 | 比赛地点 |
17年3月10日 | 新疆﹣辽宁 | 新疆 | 辽宁 | 20:00 | 乌鲁木齐 |
17年3月12日 | 新疆﹣辽宁 | 新疆 | 辽宁 | 20:00 | 乌鲁木齐 |
17年3月15日 | 辽宁﹣新疆 | 辽宁 | 新疆 | 20:00 | 本溪 |
17年3月17日 | 辽宁﹣新疆 | 辽宁 | 新疆 | 20:00 | 本溪 |
17年3月19日 | 辽宁﹣新疆 | 辽宁 | 新疆 | 20:00 | 本溪 |
17年3月22日 | 新疆﹣辽宁 | 新疆 | 辽宁 | 20:00 | 乌鲁木齐 |
17年3月24日 | 新疆﹣辽宁 | 新疆 | 辽宁 | 20:00 | 乌鲁木齐 |
(1)若考虑主场优势,每个队主场获胜的概率均为 ![]() ,客场取胜的概率均为
,客场取胜的概率均为 ![]() ,求辽宁队以比分4:1获胜的概率;
,求辽宁队以比分4:1获胜的概率;
(2)根据以往资料统计,每场比赛组织者可获得门票收入50万元(与主客场无关),若不考虑主客场因素,每个队每场比赛获胜的概率均为 ![]() ,设本次半决赛中(只考虑这两支队)组织者所获得的门票收入为X,求X的分布列及数学期望.
,设本次半决赛中(只考虑这两支队)组织者所获得的门票收入为X,求X的分布列及数学期望.