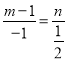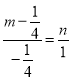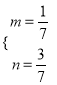题目内容
【题目】已知抛物线y2=4 ![]() x的焦点为F,A、B为抛物线上两点,若
x的焦点为F,A、B为抛物线上两点,若 ![]() =3
=3 ![]() ,O为坐标原点,则△AOB的面积为( )
,O为坐标原点,则△AOB的面积为( )
A.8 ![]()
B.4 ![]()
C.2 ![]()
D.![]()
【答案】B
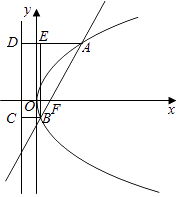
【解析】解:抛物线y2=4 ![]() x的焦点为F(
x的焦点为F( ![]() ,0),由抛物线的定义可知:|AF|=|AD|,|BC|=|BF|,
,0),由抛物线的定义可知:|AF|=|AD|,|BC|=|BF|,
过B做BE⊥AD,
由 ![]() =3
=3 ![]() ,则丨
,则丨 ![]() 丨=丨
丨=丨 ![]() 丨,
丨,
∴|AB|=2|AE|,由抛物线的对称性,不妨设直线的斜率为正,
∴直线AB的倾斜角为60°,直线AB的方程为y= ![]() (x﹣
(x﹣ ![]() )=
)= ![]() x﹣3,
x﹣3,
联立直线AB与抛物线的方程可得: ![]() ,整理得:3x2﹣10
,整理得:3x2﹣10 ![]() x+9=0,
x+9=0,
由韦达定理可知:x1+x2= ![]() ,则丨AB丨=x1+x2+p=
,则丨AB丨=x1+x2+p= ![]() +2
+2 ![]() =
= ![]() ,
,
而原点到直线AB的距离为d= ![]() =
= ![]() ,
,
则三角形△AOB的面积S= ![]() 丨AB丨d=
丨AB丨d= ![]()
![]()
![]() =4
=4 ![]() ,
,
∴当直线AB的倾斜角为120°时,同理可求S=4 ![]() ,
,
所以答案是:B.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目