题目内容
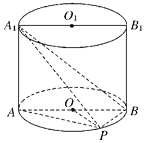
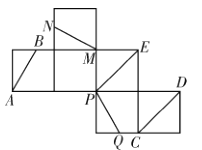
【题目】如图是一正方体的表面展开图.![]() 、
、![]() 、
、![]() 都是所在棱的中点.则在原正方体中:①
都是所在棱的中点.则在原正方体中:①![]() 与
与![]() 异面;②
异面;②![]() 平面
平面![]() ;③平面
;③平面![]() 平面
平面![]() ;④
;④![]() 与平面
与平面![]() 形成的线面角的正弦值是
形成的线面角的正弦值是![]() ;⑤二面角
;⑤二面角![]() 的余弦值为
的余弦值为![]() .其中真命题的序号是______.
.其中真命题的序号是______.
【答案】①②④
【解析】
将正方体的表面展开图还原成正方体,利用正方体中线线、线面以及面面关系,以及直线与平面所成角的定义和二面角的定义进行判断.
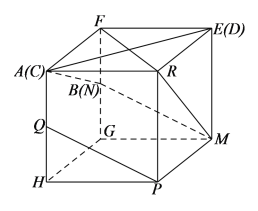
根据条件将正方体进行还原如下图所示:
对于命题①,由图形可知,直线![]() 与
与![]() 异面,命题①正确;
异面,命题①正确;
对于命题②,![]() 、
、![]() 分别为所在棱的中点,易证四边形
分别为所在棱的中点,易证四边形![]() 为平行四边形,
为平行四边形,
所以,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,命题②正确;
,命题②正确;
对于命题③,在正方体中,![]() 平面
平面![]() ,
,
由于四边形![]() 为平行四边形,
为平行四边形,![]() ,
,![]() 平面
平面![]() .
.
![]() 、
、![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
则二面角![]() 所成的角为
所成的角为![]() ,显然
,显然![]() 不是直角,
不是直角,
则平面![]() 与平面
与平面![]() 不垂直,命题③错误;
不垂直,命题③错误;
对于命题④,设正方体的棱长为![]() ,易知
,易知![]() 平面
平面![]() ,则
,则![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,由勾股定理可得
,由勾股定理可得![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,即直线
,即直线![]() 与平面
与平面![]() 所成线面角的正弦值为
所成线面角的正弦值为![]() ,命题④正确;
,命题④正确;
对于命题⑤,在正方体中,![]() 平面
平面![]() ,且
,且![]() ,
,![]() 平面
平面![]() .
.
![]() 、
、![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,
所以,二面角![]() 的平面角为
的平面角为![]() ,
,
在![]() 中,由勾股定理得
中,由勾股定理得![]() ,
,![]() ,
,
由余弦定理得![]() ,命题⑤错误.
,命题⑤错误.
故答案为:①②④.

 阅读快车系列答案
阅读快车系列答案【题目】甲、乙两个篮球队在4次不同比赛中的得分情况如下:
甲队 | 88 | 91 | 92 | 96 |
乙队 | 89 | 93 | 9▓ | 92 |
乙队记录中有一个数字模糊(即表中阴影部分),无法确认,假设这个数字具有随机性,并用![]() 表示.
表示.
(Ⅰ)在4次比赛中,求乙队平均得分超过甲队平均得分的概率;
(Ⅱ)当![]() 时,分别从甲、乙两队的4次比赛中各随机选取1次,记这2个比赛得分之差的绝对值为
时,分别从甲、乙两队的4次比赛中各随机选取1次,记这2个比赛得分之差的绝对值为![]() ,求随机变量
,求随机变量![]() 的分布列;
的分布列;
(Ⅲ)如果乙队得分数据的方差不小于甲队得分数据的方差,写出![]() 的取值集合.(结论不要求证明)
的取值集合.(结论不要求证明)
【题目】现行的个税法修正案规定:个税免征额由原来的2000元提高到3500元,并给出了新的个人所得税税率表:
全月应纳税所得额 | 税率 |
不超过1500元的部分 | 3% |
超过1500元至4500元的部分 | 10% |
超过4500元至9000元的部分 | 20% |
超过9000元至35000元的部分 | 25% |
…… | … |
例如某人的月工资收入为5000元,那么他应纳个人所得税为:![]() (元).
(元).
(Ⅰ)若甲的月工资收入为6000元,求甲应纳的个人收的税;
(Ⅱ)设乙的月工资收入为![]() 元,应纳个人所得税为
元,应纳个人所得税为![]() 元,求
元,求![]() 关于
关于![]() 的函数;
的函数;
(Ⅲ)若丙某月应纳的个人所得税为1000元,给出丙的月工资收入.(结论不要求证明)