Question

【题目】在正方体AC1中，E，F分别为D1C1，B1C1的中点，AC∩BD＝P，A1C1∩EF＝Q，如图.

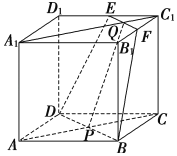
（1）若A1C交平面EFBD于点R，证明:P，Q，R三点共线.

（2）线段AC上是否存在点M，使得平面B1D1M∥平面EFBD，若存在确定M的位置，若不存在说明理由.

Answer 1

【答案】（1）证明见解析（2）存在；M为AP中点

【解析】

根据题意,证明P，Q，R是平面BDEF和平面BDD1B1的公共点,利用平面的公理3即可得证;

存在点M为AP中点, 使平面B1D1M∥平面EFBD.取AD中点G，AB中点H，连结GH，交AC于点M，连结D1G，B1H,利用线面平行的判定定理证明平面，平面,由面面平行的判定定理即可得证.

（1）证明：∵在正方体AC1中，E，F分别为D1C1，B1C1的中点，

AC∩BD＝P，A1C1∩EF＝Q，A1C交平面EFBD于点R，

∴P，Q，R是平面BDEF和平面BDD1B1的公共点，

∴P，Q，R三点共线.

（2）存在点M为AP中点, 使平面B1D1M∥平面EFBD.

证明如下:取AD中点G，AB中点H，连结GH，交AC于点M，连结D1G，B1H，如图:

由题意得,GH∥EF,因为平面,平面，

所以平面,

因为B1H∥DE,同理可证,平面,

又因为, 由面面平行的判定定理可得,

∴平面GHB1D1∥平面BDEF，

∴线段AC上存在点M，使得平面B1D1M∥平面EFBD，且M为AP中点.