题目内容
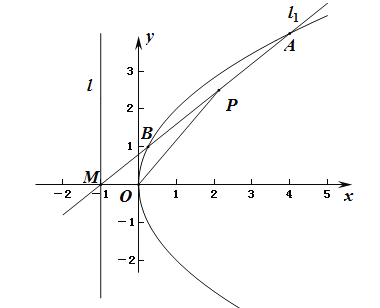
【题目】如图,过抛物线C:y2=2px(p>0)的准线l上的点M(﹣1,0)的直线l1交抛物线C于A,B两点,线段AB的中点为P.
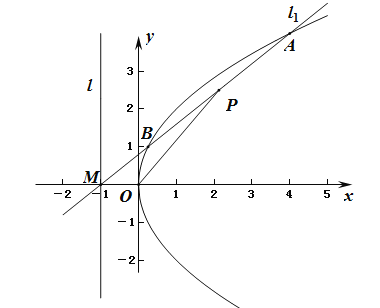
(Ⅰ)求抛物线C的方程;
(Ⅱ)若|MA||MB|=λ|OP|2,求实数λ的取值范围.
【答案】(Ⅰ)y2=4x;(Ⅱ)λ∈(0,![]() ).
).
【解析】
(Ⅰ)由题意得抛物线方程;
(Ⅱ)设直线![]()
![]() 与联立抛物线,由设而不求的方法得点
与联立抛物线,由设而不求的方法得点![]() 横纵坐标的关系,计算
横纵坐标的关系,计算![]() 的值,得出参数
的值,得出参数![]() 的取值范围.
的取值范围.
(Ⅰ)抛物线的准线方程为:x=﹣1,所以抛物线C的方程为:y2=4x;
(Ⅱ)设直线l1的方程为:x=my﹣1,代入抛物线中得:
y2﹣4my+4=0,△=16m2﹣16>0,∴m2>1,
设A(x,y),B(x',y'),
∴y+y'=4m,yy'=4,
|MA||MB|![]() |y﹣yM|
|y﹣yM|![]() |y'﹣yM|=(1+m2)|yy'|=4(1+m2),
|y'﹣yM|=(1+m2)|yy'|=4(1+m2),
AB的中点P的坐标(2m2﹣1,2m),|OP|2=(2m2﹣1)2+4m2=4m4+1,
|MA||MB|=λ|OP|2λ ,
,
令m2+1=t(t>2),
则λ 在(2,+∞)上是减函数,
在(2,+∞)上是减函数,
故λ∈(0,![]() ).
).

练习册系列答案
相关题目