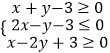题目内容
【题目】函数![]()
(1)讨论![]() 的单调性;
的单调性;
(2)若函数![]() 有两个极值点
有两个极值点![]() ,且
,且![]() ,求证:
,求证: ![]()
【答案】(1) ![]() 时,
时, ![]() 在
在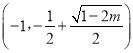 上单减,在
上单减,在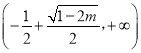 上单增;
上单增; ![]() 时,
时, ![]() 在
在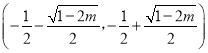 上单减,在
上单减,在 和
和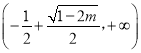 上单增;
上单增; ![]() 时,
时, ![]() 在
在![]() 上单增;(2)见解析.
上单增;(2)见解析.
【解析】试题分析:(1) ![]() ,分类讨论,研究
,分类讨论,研究![]() 的符号情况,进而得到函数的单调区间;(2) 设函数
的符号情况,进而得到函数的单调区间;(2) 设函数![]() 有两个极值点
有两个极值点![]() ,且
,且![]() ,
, ![]()
![]() 、
、![]() 是
是![]() 的二根
的二根![]()
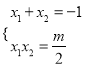 ,若证
,若证![]() 成立,只需证
成立,只需证![]() 对
对![]() 恒成立.设
恒成立.设![]() ,研究其最值即可.
,研究其最值即可.
试题解析:
解: ![]() 的定义域是
的定义域是![]() ,
,![]()
(1)由题设知, ![]()
令![]() ,这是开口向上,以
,这是开口向上,以![]() 为对称轴的抛物线.
为对称轴的抛物线.
在![]() 时,当
时,当![]() ,即
,即![]() 时,
时, ![]() ,即
,即![]() 在
在![]() 上恒成立.
上恒成立.
②当![]() ,即
,即![]() 时,由
时,由![]() 得
得![]()
令![]() ,
, ![]()
则![]() ,
, ![]()
1) 当![]() 即
即![]() ,即
,即![]() 时,
时,
![]() 时,
时, ![]() ,即
,即![]() ,
, ![]() 时,
时, ![]() ,即
,即![]()
2) 当![]() 时,即
时,即![]() ,即
,即![]() 时
时
![]() 时,
时, ![]() ,即
,即![]()
![]() 或
或![]() 时,
时, ![]() ,即
,即![]()
综上:
![]() 时,
时, ![]() 在
在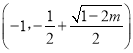 上单减,在
上单减,在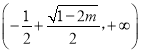 上单增;
上单增;
![]() 时,
时, ![]() 在
在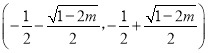 上单减,在
上单减,在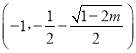 和
和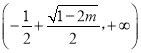 上单增;
上单增; ![]() 时,
时, ![]() 在
在![]() 上单增.
上单增.
(2)若函数![]() 有两个极值点
有两个极值点![]() ,且
,且![]()
则必是![]() ,则
,则![]() ,则
,则![]() ,
,
且![]() 在
在![]() 上单减,在
上单减,在![]() 和
和![]() 上单增,
上单增,
则![]()
![]()
![]() 、
、![]() 是
是![]() 的二根
的二根
![]()
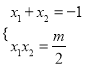 ,即
,即![]() ,
, ![]()
![]() 若证
若证![]() 成立,只需证
成立,只需证
![]()
![]()
![]()
即证![]() 对
对![]() 恒成立
恒成立
设![]()
![]()
当![]() 时,
时, ![]() ,
, ![]() ,
, ![]()
故![]() ,故
,故![]() 在
在![]() 上单增
上单增
故![]()
![]()
![]() 对
对![]() 恒成立
恒成立
![]()
![]()

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目