题目内容
【题目】如图,在三棱锥P﹣ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC的中点,它的正(主)视图和侧(左)视图如图所示. 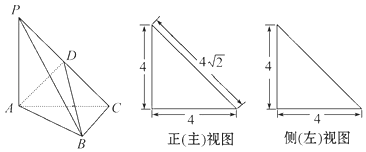
(Ⅰ)求三棱锥P﹣ABD的体积.
(Ⅱ)在∠ACB的平分线所在直线上确定一点Q,使得PQ∥平面ABD,并求此时PQ的长.
【答案】解:(Ⅰ)由已知可得:
三棱锥P﹣ABD的底面ABC中,AC=BC=4,AC⊥BC,
高PA=4,
故三棱锥P﹣ABD体积V= ![]() ×
× ![]() ×4×4×4=
×4×4×4= ![]() ;
;
(Ⅱ)解:如图取AB的中点O,连接CO并延长至Q,使得CQ=2CO,点Q即为所求.
因为O为CQ中点,所以PQ∥OD,
因为PQ平面ABD,OD平面ABD,所以PQ∥平面ABD
连接AQ,BQ,四边形ACBQ的对角线互相平分,
所以ACBQ为平行四边形,所以AQ=4,…(11分)
又PA⊥平面ABC,
所以在直角△PAQ中,PQ= ![]() =4
=4 ![]() .
.
【解析】(Ⅰ)由已知中的三视图,得到棱锥的底面边长和高,代入棱锥体积公式,可得答案;(Ⅱ)取AB的中点O,连接CO并延长至Q,使得CQ=2CO,利用线面平行的判定可知点Q即为所求,证明ACBQ为平行四边形,即可求出PQ的长
【考点精析】关于本题考查的由三视图求面积、体积和直线与平面平行的判定,需要了解求体积的关键是求出底面积和高;求全面积的关键是求出各个侧面的面积;平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能得出正确答案.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目




