题目内容
【题目】已知三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]()
![]()
![]() 则三棱锥
则三棱锥![]() 的外接球的表面积为__________.
的外接球的表面积为__________.
【答案】![]()
【解析】
利用已知三棱锥A﹣BCD的特点AB=AD,先确定△ABD的外心O,及外接圆的半径,然后证明O也是三棱锥A﹣BCD的外接球的球心,从而得到外接球的半径,即可得到外接球表面积.
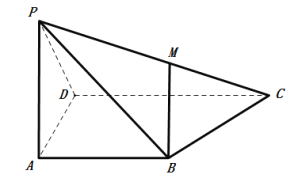
如图取BD的中点E,连接AE,CE,则AE⊥BD,CE⊥BD.
∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,∴AE⊥平面BCD,
又∵CE平面BCD,∴AE⊥CE.
设△ABD的外接圆的圆心为O,半径为r.
∵AB=AD,∴圆心O在AE所在的直线上.
∴r2=BE2+OE2=BE2+(r﹣AE)2.
∵在Rt△BCD中,BD=![]() =4
=4![]() ,∴BE=EC=2
,∴BE=EC=2![]() .
.
∴在Rt△ABE中,AE=![]() =2.∴r2=8+(r﹣2)2,解得r=3,∴OE=1.
=2.∴r2=8+(r﹣2)2,解得r=3,∴OE=1.
在Rt△OEC中,OC=![]() =3,∴OA=OB=OC=OD=3.
=3,∴OA=OB=OC=OD=3.
∴点O是三棱锥A﹣BCD的外接球的球心,且球半径R=3.
∴球的表面积S=4πR2=36π.
故答案为:36π

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】为了解某市的交通状况,现对其6条道路进行评估,得分分别为:5,6,7,8,9,10.规定评估的平均得分与全市的总体交通状况等级如表
评估的平均得分 | (0,6] | (6,8] | (8,10] |
全市的总体交通状况等级 | 不合格 | 合格 | 优秀 |
(1)求本次评估的平均得分,并参照上表估计该市的总体交通状况等级.
(2)用简单随机抽样方法从这6条道路中抽取2条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的绝对值不超0.5的概率.