Question

【题目】已知椭圆以坐标原点为中心，焦点在轴上，焦距为2，且经过点.

（1）求椭圆的方程；

（2）设点，点为曲线上任一点，求点到点距离的最大值；

（3）在（2）的条件下，当时，设的面积为（O是坐标原点，Q是曲线C上横坐标为a的点），以为边长的正方形的面积为，若正数满足，问是否存在最小值，若存在，请求出此最小值，若不存在，请说明理由.

Answer 1

【答案】（1）（2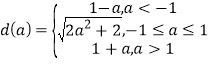） (3) m存在最小值

【解析】

（1）根据已知求出a，b，c值，可得椭圆C的方程；（2）设P（x，y），则y2＝2﹣2x2，利用两点间的距离公式可得|PA|2＝（x﹣a）2+y2＝（x﹣a）2+2﹣2x2，转为二次函数求最值问题；（3）由题意分别表示出S1及S2，对不等式S1≤mS2进行变量分离得到，令，通过换元t＝a2+1转为二次函数求最值问题．

（1）由题意知c=1,又过点（1,0）所以b=1,故a=,则椭圆方程为.

（2）设，则

令，

所以当时在[-1，1]上是减函数，

；

当时，在上是增函数，

在上是减函数，则；

当时，在上是增函数；

所以.

（3）当时，，

.

若正数m满足条件，

则，即，

，令，

设，则，.

，

所以，当，即时，

即，.所以，m存在最小值

【另解】

由，得，

而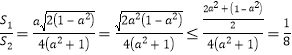

当且仅当，

即，等号成立，∴

从而，故m的最小值为