题目内容
【题目】已知F是椭圆C： 
+ 
=1的右焦点，P是C上一点，A（﹣2，1），当△APF周长最小时，其面积为 ．
【答案】4
【解析】解：椭圆C： 
+ 
=1的a=2 
，b=2，c=4， 设左焦点为F'（﹣4，0），右焦点为F（4，0）．
△APF周长为|AF|+|AP|+|PF|=|AF|+|AP|+（2a﹣|PF'|）
=|AF|+|AP|﹣|PF'|+2a≥|AF|﹣|AF'|+2a，
当且仅当A，P，F'三点共线，即P位于x轴上方时，三角形周长最小．
此时直线AF'的方程为y= 
（x+4），代入x2+5y2=20中，可求得P（0，2），
故S△APF=S△PF'F﹣S△AF'F= ×2×8﹣ ×1×8=4．
所以答案是：4．
中考解读考点精练系列答案
【题目】在某校组织的一次篮球定点投篮训练中，规定每人最多投3次；在A处每投进一球得3分，在B处每投进一球得2分；如果前两次得分之和超过3分即停止投篮，否则投第三次，某同学在A处的命中率q1为0.25，在B处的命中率为q2 ， 该同学选择先在A处投一球，以后都在B处投，用ξ表示该同学投篮训练结束后所得的总分，其分布列为：
ξ | 0 | 2 | 3 | 4 | 5 |
p | 0.03 | 0.24 | 0.01 | 0.48 | 0.24 |
（1）求q2的值；
（2）求随机变量ξ的数学期望Eξ；
（3）试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小．
【题目】某市司法部门为了宣传《宪法》举办法律知识问答活动，随机对该市18～68岁的人群抽取一个容量为n的样本，并将样本数据分成五组：[18，28），[28，38），[38，48），[48，58），[58，68），再将其按从左到右的顺序分别编号为第1组，第2组，…，第5组，绘制了样本的频率分布直方图；并对回答问题情况进行统计后，结果如下表所示．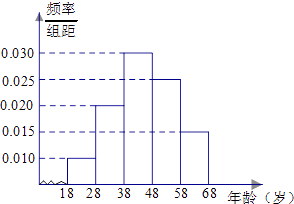
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的比例 |
第1组 | [18，28） | 5 | 0.5 |
第2组 | [28，38） | 18 | a |
第3组 | [38，48） | 27 | 0.9 |
第4组 | [48，58） | x | 0.36 |
第5组 | [58，68） | 3 | 0.2 |
（1）分别求出a，x的值；
（2）从第2，3，4组回答正确的人中用分层抽样方法抽取6人，则第2，3，4组每组应各抽取多少人？
（3）在（2）的前提下，决定在所抽取的6人中随机抽取2人颁发幸运奖，求：所抽取的人中第2组至少有1人获得幸运奖的概率．
【题目】某单位为了了解办公楼用电量y（度）与气温x（℃）之间的关系，随机统计了四个工作日的用电量与当天平均气温，并制作了对照表：
气温（℃） | 17 | 14 | 11 | ﹣2 |
用电量（度） | 23 | 35 | 39 | 63 |
由表中数据得到线性回归方程 
=﹣2x+a，当气温为﹣5℃时，预测用电量约为 （ ）
A.38度
B.50度
C.70度
D.30度
