题目内容
【题目】定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M>0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的上界.已知函数 ![]() .
.
(1)若f(x)是奇函数,求m的值;
(2)当m=1时,求函数f(x)在(﹣∞,0)上的值域,并判断函数f(x)在(﹣∞,0)上是否为有界函数,请说明理由;
(3)若函数f(x)在[0,1]上是以3为上界的函数,求实数m的取值范围.
【答案】
(1)解:由f(x)是奇函数,则f(﹣x)=﹣f(x)
得 ![]() ,即(1﹣m2)2x=0,∴m2﹣1=0,m=±1
,即(1﹣m2)2x=0,∴m2﹣1=0,m=±1
(2)解:当m=1时, ![]() .
.
∵x<0,∴0<2x<1,∴f(x)∈(0,1),满足|f(x)|≤1.
∴f(x)在(﹣∞,0)上为有界函数
(3)解:若函数f(x)在[0,1]上是以3为上界的有界函数,则有|f(x)|≤3在[0,1]上恒成立.
∴﹣3≤f(x)≤3,
即 ![]() ,
,
∴ 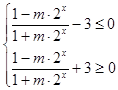 ,化简得:
,化简得: 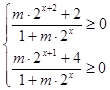 ,
,
即 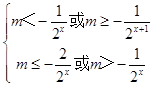 ,
,
上面不等式组对一切x∈[0,1]都成立,
故  ,
,
∴ ![]()
【解析】(1)根据函数奇偶性的性质建立方程关系进行求解即可.(2)根据分式函数的性质以及有界函数的定义进行求解判断即可.(3)根据函数的有界性建立不等式关系,利用不等式恒成立进行求解即可.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案【题目】在某校组织的一次篮球定点投篮训练中,规定每人最多投3次;在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投第三次,某同学在A处的命中率q1为0.25,在B处的命中率为q2 , 该同学选择先在A处投一球,以后都在B处投,用ξ表示该同学投篮训练结束后所得的总分,其分布列为:
ξ | 0 | 2 | 3 | 4 | 5 |
p | 0.03 | 0.24 | 0.01 | 0.48 | 0.24 |
(1)求q2的值;
(2)求随机变量ξ的数学期望Eξ;
(3)试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小.
【题目】某单位为了了解办公楼用电量y(度)与气温x(℃)之间的关系,随机统计了四个工作日的用电量与当天平均气温,并制作了对照表:
气温(℃) | 17 | 14 | 11 | ﹣2 |
用电量(度) | 23 | 35 | 39 | 63 |
由表中数据得到线性回归方程 ![]() =﹣2x+a,当气温为﹣5℃时,预测用电量约为 ( )
=﹣2x+a,当气温为﹣5℃时,预测用电量约为 ( )
A.38度
B.50度
C.70度
D.30度