题目内容
判断圆C1:x2+y2-2x-6y-26=0与圆C2:x2+y2-4x+2y+4=0?的公切线条数.
圆C1与圆C2没有公切线.
由题意,得将圆C1化为标准方程为(x-1)2+(y-3)2=36,
将圆C2化为标准方程为(x-2)2+(y+1)2=1,
得圆C1的圆心坐标C1(1,3),半径r1=6,
圆C2的圆心坐标C2(2,-1),半径r2=1,
∴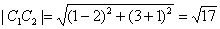 .
.
又|C1C2|<r1-r2,即两圆内含,
∴圆C1与圆C2没有公切线.
将圆C2化为标准方程为(x-2)2+(y+1)2=1,
得圆C1的圆心坐标C1(1,3),半径r1=6,
圆C2的圆心坐标C2(2,-1),半径r2=1,
∴
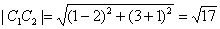 .
.又|C1C2|<r1-r2,即两圆内含,
∴圆C1与圆C2没有公切线.

练习册系列答案
相关题目
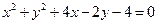 ,则
,则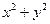 的最大值是 .
的最大值是 . 与圆
与圆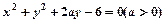 的公共弦的长为
的公共弦的长为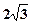 ,则
,则 ( )
( )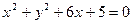 外切,同时与圆
外切,同时与圆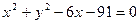 内切,则动圆圆心的轨迹方程是[
内切,则动圆圆心的轨迹方程是[