题目内容
圆C1:x2+y2=1与圆C2:x2+y2-4x+2y+1=0的位置关系为______.
由圆C1:x2+y2=1,圆心C1(0,0),且R=1,
圆C2:x2+y2-4x+2y+1=0,
得到圆心C2(2,-1),r=2,
∴两圆心间的距离d=
=
<2+1,
∵1<
<3,即r-R<d<R+r,
∴圆C1和圆C2的位置关系是相交.
故答案为:相交.
圆C2:x2+y2-4x+2y+1=0,
得到圆心C2(2,-1),r=2,
∴两圆心间的距离d=
| (2-0)2+(-1-0)2 |
| 5 |
∵1<
| 5 |
∴圆C1和圆C2的位置关系是相交.
故答案为:相交.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
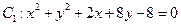 ,圆
,圆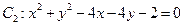 ,
,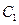 与圆
与圆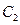 的关系。
的关系。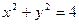 与圆
与圆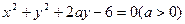 的公共弦长为
的公共弦长为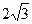 ,则a=________.
,则a=________.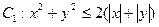 内,动点Q在曲线
内,动点Q在曲线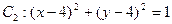 上,则平面区域
上,则平面区域 的面积是_________,
的面积是_________,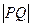 的最小值为__________.
的最小值为__________.