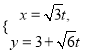题目内容
【题目】某调查机构对本市小学生课业负担情况进行了调查，设平均每人每天做作业的时间为
分钟，有1200名小学生参加了此项调查，调查所得到的数据用程序框图处理（如图），若输出的结果是840，若用样本频率估计概率，则平均每天做作业的时间在0～60分钟内的学生的概率是（ ）
A. 0.32 B. 0.36 C. 0.7 D. 0.84
【答案】A
【解析】
由程序框图和题意，分析该程序的作用，即可求解.
由程序框图可知：该程序的作用是统计1000名学生中，平均每天做作业的时间不在0～60分钟内的学生的人数.由输出结果为680，则平均每天做作业的时间在0～60分钟内的学生人数为1000-680=320，
故平均每天做作业的时间在0～60分钟内的学生的概率是
,
故选A.
【题目】房产税改革向前推进之路，虽历经坎坷,但步伐从未停歇，作为未来的新增税种,十二届全国人大常委会已将房产税立法正式列入五年立法规划。某市税务机关为了进一步了解民众对政府择机出台房产税的认同情况，随机抽取了一小区住户进行调查,各户人均月收入(单位：千元)的频数分布及赞成出台房产税的户数如下表：
人均月收入 |
|
|
|
|
|
|
频数 | 6 | 10 | 13 | 11 | 8 | 2 |
不赞成户数 | 5 | 9 | 12 | 9 | 4 | 1 |
若将小区人均月收入不低于7.5千元的住户称为“高收入户”,人均月收入低于7.5千元的住户称为“非高收入户”,有
列联表:
非高收入户 | 高收入户 | 总计 | |
不赞成 | |||
赞成 | |||
总计 |
（1）根据已知条件完成如图所给的列联表，并说明能否在犯错误的概率不超过0.005的前提下认为“收入的高低”与“赞成出台房产税”有关.
（2）现从月收入在
的住户中随机抽取两户，求所抽取的两户都不赞成出台房产税的概率；
附：临界值表
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式：
.
