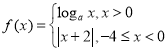题目内容
【题目】（1）已知函数
，其中
，求函数
的图象恰好经过第一、二、三象限的概率；
（2）某校早上8:10开始上课，假设该校学生小张与小王在早上7:30～8:00之间到校，且每人到该时间段内到校时刻是等可能的，求两人到校时刻相差10分钟以上的概率.
【答案】（1）
（2）
【解析】
(1)先求出函数
的系数
构成的数对的个数，再求出满足题意的数对的个数，由古典概型的概率公式即可求出结果;
(2)先设小张和小王到校时刻分别为
，依题意确定的关系，作出对于图像，由几何概型的计算公式，即可求解.
（1）设函数的系数构成的数对为
，则由题意知数对可能为：
，
，
共16种情况.
要使得函数的图象经过第一，二，三象限，则需
，即
符合条件的数对为，
共3对.
模型符合古典概型的定义，所以所求事件的概率为.
（2）设小张和小王到校时刻分别为，且
.
两人到校时刻相差10分钟等价于
，且.
模型符合几何概型的定义，由图可知：
所以所求事件的概率为
.
练习册系列答案
相关题目
