在正方体的8个顶点.12条棱的中点.6个面的中心及正方体的中心共27个点中.共线的三点组的个数是49．题目和参考答案——青夏教育精英家教网—

题目内容

13．在正方体的8个顶点，12条棱的中点，6个面的中心及正方体的中心共27个点中，共线的三点组的个数是49．

分析根据题意，结合正方体的结构特征，分3种情况讨论：①、三点都在正方体的棱上，②、以6个面的中心为中点，③、以正方体的中心为中点，分别求出每种情况下三点共线的情况数目，由分类计数原理计算可得答案．

解答解：根据题意，在所给的正方体的27个点中，三点共线的情况有3种：
①、三点都在正方体的棱上，正方体有12条棱，即有12种情况；
②、以6个面的中心为中点，正方体有6个面，每个面有4种情况，共有4×6=24种情况，
③、以正方体的中心为中点，共有26÷2=13种情况，
则共有12+24+13=49种，即共线的三点组的个数是49；
故答案为：49．

点评本题考查分类计数原理的应用，解题的关键在于掌握正方体的结构特点并判断三点共线的情况．

练习册系列答案

4．若2013的每个质因子都是某个正整数等差数列{a_n}中的项，则a₂₀₁₃的最大值是4027．

1．已知不等式组$\left\{\begin{array}{l}{2x-y+4≥0}\\{x+y-3≤0}\\{y≥0}\end{array}\right.$构成平面区域Ω（其中x，y是变量），若目标函数z=ax+6y（a＞0）的最小值为-6，则实数a的值为（　　）

8．已知在平面直角坐标系xoy上的区域D由不等式组$\left\{{\begin{array}{l}{1≤x≤2}\\{y≤2}\\{2x-y≤2}\end{array}}\right.$给定．若M（x，y）为D上的动点，点A的坐标为（2，1），则z=$\overrightarrow{OA}•\overrightarrow{AM}$的最大值为（　　）

18．已知m，4，n是等差数列，那么${（\sqrt{2}）^m}•{（\sqrt{2}）^n}$=16；mn的最大值为16．

5．若x，y∈R，则x＞y的一个充分不必要条件是（　　）

x²＞y²

x³＞y³

	A．	“p∨q为真”是“p∧q为真”的充分不必要条件
	B．	若数据x₁，x₂，x₃，…，x_n的方差为1，则2x₁，2x₂，2x₃，…，2x_n的方差为2
	C．	命题“存在x∈R，x²+x+2015＞0”的否定是“任意x∈R，x²+x+2015＜0”
	D．	在区间[0，π]上随机取一个数x，则事件“sinx+cosx≥$\frac{\sqrt{6}}{2}$”发生的概率为$\frac{1}{3}$

3．

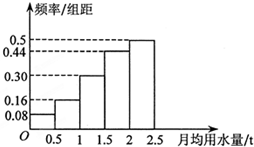如图是绵阳市某小区100户居民2014年月平均用水量（单位：t）的频率分布直方图的一部分，则该小区2014年的月平均用水量的中位数的估计值为2.02．

试题分类