题目内容
【题目】已知数列{an}是公差不为0的等差数列，数列{bn}是等比数列，且b1=a1=1，b2=a3 ， b3=a9
（1）求数列{an}的通项公式；
（2）求数列{anbn}的前n项和Sn ．
【答案】
（1）解：设等差数列{an}的公差为d≠0，等比数列{bn}的公比为q，且b1=a1=1，b2=a3，b3=a9，
∴q=1+2d，q2=1+8d，解得q=3，d=1．
∴an=1+（n﹣1）=n．
（2）解：由（1）可得：bn=3n﹣1．
∴anbn=n3n﹣1．
数列{anbn}的前n项和Sn=1+2×3+3×32+…+n3n﹣1．
∴3Sn=3+2×32+…+（n﹣1）3n﹣1+n3n，
∴﹣2Sn=1+3+32+…+3n﹣1﹣n3n= 
﹣n3n= 
3n﹣ 
，
∴Sn= 
+ 
．
【解析】（1）利用等差数列与等比数列的通项公式即可得出；（2）由（1）可得：bn=3n﹣1 ． anbn=n3n﹣1 ． 再利用“错位相减法”与等比数列的前n项和公式即可得出．
【考点精析】通过灵活运用等差数列的通项公式（及其变式）和数列的前n项和，掌握通项公式：
或
；数列{an}的前n项和sn与通项an的关系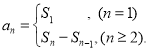
即可以解答此题．
阅读快车系列答案
【题目】一个化肥厂生产甲种混合肥料1车皮、乙种混合肥料1车皮所需要的主要原料如表：
原料 | 磷酸盐（单位：吨） | 硝酸盐（单位：吨） |
甲 | 4 | 20 |
乙 | 2 | 20 |
现库存磷酸盐8吨、硝酸盐60吨，计划在此基础上生产若干车皮的甲、乙两种混合肥料．
（1）设x，y分别表示计划生产甲、乙两种肥料的车皮数，试列出x，y满足的数学关系式，并画出相应的平面区域；
（2）若生产1车皮甲种肥料，利润为3万元；生产1车皮乙种肥料，利润为2万元．那么分别生产甲、乙两种肥料多少车皮，能够产生最大利润？最大利润是多少？
