题目内容
已知双曲线
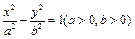 的离心率为e,右顶点为A,左、右焦点分别为
的离心率为e,右顶点为A,左、右焦点分别为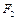 、
、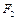 ,点E为右准线上的动点,
,点E为右准线上的动点,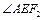 的最大值为
的最大值为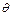 .
.(1)若双曲线的左焦点为
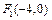 ,一条渐近线的方程为
,一条渐近线的方程为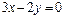 ,求双曲线的方程;
,求双曲线的方程;(2)求
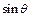 (用
(用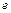 表示);
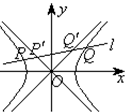
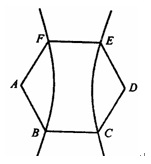
表示);(3)如图,如果直线l与双曲线的交点为P、Q,与两条渐近线的交点为
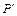 、
、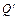 ,O为坐标原点,求证:
,O为坐标原点,求证: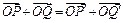
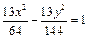 ,
,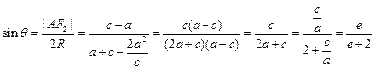
解:(1)方法1 设双曲线的方程为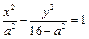 ,则其渐近线的方程为
,则其渐近线的方程为 ,即
,即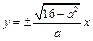 .又∵一条渐近线的方程是
.又∵一条渐近线的方程是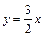 ,∴
,∴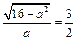 ,得
,得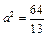 ,
,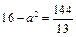 .故双曲线的方程为
.故双曲线的方程为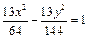 .
.
方法2 ∵双曲线的一条渐近线是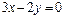 ,即
,即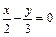 ,∴可设双曲线的方程为
,∴可设双曲线的方程为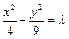 .∵焦点是
.∵焦点是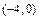 ,∴由
,∴由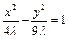 得
得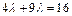 ,∴
,∴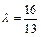 ,∴双曲线的方程为
,∴双曲线的方程为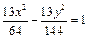 .
.
 (2)设经过点A、
(2)设经过点A、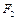 的圆C与准线相切于点M,交
的圆C与准线相切于点M,交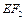 于点N.
于点N.
∵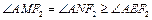 (当E与M重合时取“=”),
(当E与M重合时取“=”),
∴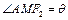 .∵
.∵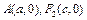 ,∴
,∴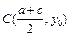 ,又∵
,又∵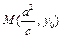 ,
,
∴圆C的半径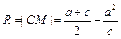 .由正弦定理得
.由正弦定理得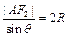 ,
,
∴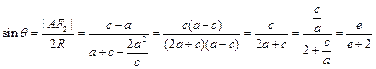 .
.
(3)证明:方法1 当直线l的斜率存在时,设直线l的方程为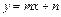 ,代入
,代入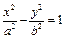 中得
中得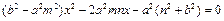 .设
.设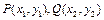 ,线段PQ的中点为
,线段PQ的中点为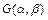 ,则
,则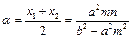 .同理,将
.同理,将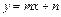 代入渐近线方程
代入渐近线方程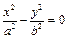 中得
中得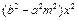
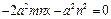 .设
.设 ,线段
,线段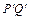 的中点为
的中点为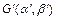 ,则
,则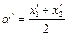
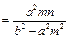 ,∴
,∴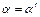 ,即线段PQ与线段
,即线段PQ与线段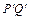 有共同的中点.当直线l的斜率不存在时,即直线l垂直于x轴时,由对称性可知线段PQ与线段
有共同的中点.当直线l的斜率不存在时,即直线l垂直于x轴时,由对称性可知线段PQ与线段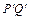 有共同的中点.∴
有共同的中点.∴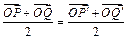 ,即
,即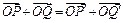 .
.


方法2 当直线l的斜率不存在或为零时,即直线l垂直于x轴或垂直于y轴时,由对称性可知线段PQ与线段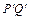 有共同的中点,∴
有共同的中点,∴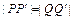 .
.
当直线l的斜率存在且不为零时,可设l: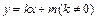 .设PQ的中点为
.设PQ的中点为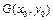 ,
,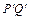 的中点为
的中点为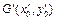 ,则由点差法可得
,则由点差法可得 ,且
,且 ,∴点G、
,∴点G、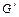 在直线
在直线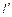 :
: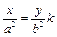 ,即
,即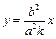 上.又∵点G、
上.又∵点G、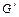 在直线l:
在直线l: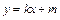 上,∴点G、
上,∴点G、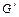 同为直线
同为直线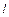 与
与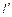 的交点.
的交点.
故点G、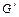 重合,∴
重合,∴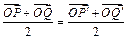 ,即
,即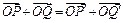 .
.
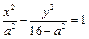 ,则其渐近线的方程为
,则其渐近线的方程为 ,即
,即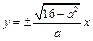 .又∵一条渐近线的方程是
.又∵一条渐近线的方程是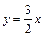 ,∴
,∴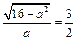 ,得
,得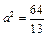 ,
,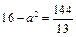 .故双曲线的方程为
.故双曲线的方程为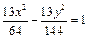 .
.方法2 ∵双曲线的一条渐近线是
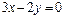 ,即
,即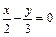 ,∴可设双曲线的方程为
,∴可设双曲线的方程为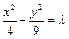 .∵焦点是
.∵焦点是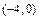 ,∴由
,∴由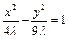 得
得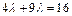 ,∴
,∴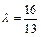 ,∴双曲线的方程为
,∴双曲线的方程为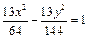 .
. (2)设经过点A、
(2)设经过点A、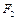 的圆C与准线相切于点M,交
的圆C与准线相切于点M,交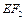 于点N.
于点N.∵
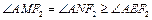 (当E与M重合时取“=”),
(当E与M重合时取“=”),∴
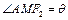 .∵
.∵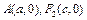 ,∴
,∴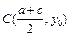 ,又∵
,又∵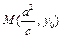 ,
,∴圆C的半径
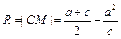 .由正弦定理得
.由正弦定理得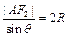 ,
,∴
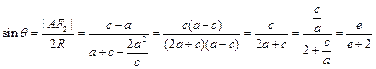 .
.(3)证明:方法1 当直线l的斜率存在时,设直线l的方程为
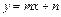 ,代入
,代入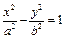 中得
中得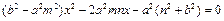 .设
.设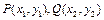 ,线段PQ的中点为
,线段PQ的中点为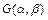 ,则
,则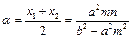 .同理,将
.同理,将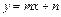 代入渐近线方程
代入渐近线方程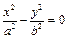 中得
中得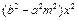
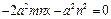 .设
.设 ,线段
,线段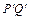 的中点为
的中点为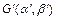 ,则
,则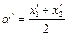
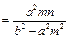 ,∴
,∴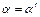 ,即线段PQ与线段
,即线段PQ与线段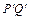 有共同的中点.当直线l的斜率不存在时,即直线l垂直于x轴时,由对称性可知线段PQ与线段
有共同的中点.当直线l的斜率不存在时,即直线l垂直于x轴时,由对称性可知线段PQ与线段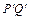 有共同的中点.∴
有共同的中点.∴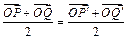 ,即
,即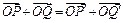 .
.


方法2 当直线l的斜率不存在或为零时,即直线l垂直于x轴或垂直于y轴时,由对称性可知线段PQ与线段
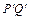 有共同的中点,∴
有共同的中点,∴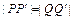 .
.当直线l的斜率存在且不为零时,可设l:
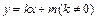 .设PQ的中点为
.设PQ的中点为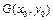 ,
,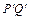 的中点为
的中点为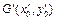 ,则由点差法可得
,则由点差法可得 ,且
,且 ,∴点G、
,∴点G、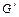 在直线
在直线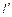 :
: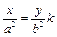 ,即
,即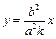 上.又∵点G、
上.又∵点G、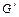 在直线l:
在直线l: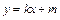 上,∴点G、
上,∴点G、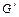 同为直线
同为直线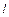 与
与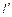 的交点.
的交点.故点G、
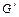 重合,∴
重合,∴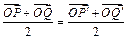 ,即
,即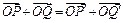 .
.
练习册系列答案
相关题目
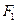 、
、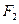 为双曲线C:
为双曲线C: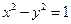 的左、右焦点,点P在C上,∠
的左、右焦点,点P在C上,∠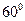 ,则P到x轴的距离为
,则P到x轴的距离为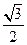
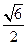
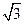
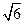
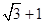 B.
B.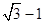
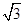 D.
D.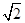
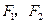 分别为双曲线
分别为双曲线 的左、右焦点,
的左、右焦点,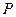 为双曲线右支上任一点,若
为双曲线右支上任一点,若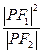 的最小值为
的最小值为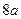 ,则该双曲线的离心率的取值范围是 ( )
,则该双曲线的离心率的取值范围是 ( )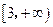

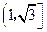
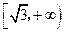
 中,
中,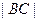 =2
=2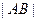 ,∠
,∠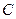 的双曲线的离心率为 ( )
的双曲线的离心率为 ( )
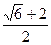
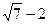
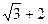
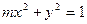 的虚轴长是实轴长的2倍,那么其中一个焦点坐标为( )
的虚轴长是实轴长的2倍,那么其中一个焦点坐标为( )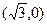
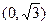
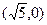
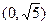
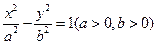 的右焦点为
的右焦点为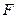 ,右准线与双曲线渐近线交于
,右准线与双曲线渐近线交于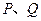 两点,如果
两点,如果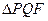 是直角三角形,则双曲线的离心率
是直角三角形,则双曲线的离心率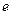 为 .
为 .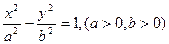 的一条渐近线方程为
的一条渐近线方程为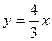 ,则双曲线的离
,则双曲线的离
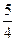
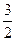
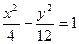 上一点P到它的右焦点的距离是8,那么点P到它的左焦点的距离是( )
上一点P到它的右焦点的距离是8,那么点P到它的左焦点的距离是( )