题目内容
【题目】如图,在平面直角坐标系中,锐角![]() 和钝角
和钝角![]() 的终边分别与单位圆交于
的终边分别与单位圆交于![]() 两点.
两点.
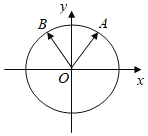
(Ⅰ)如果点![]() 纵坐标分别为
纵坐标分别为![]() ,求
,求![]() ;
;
(Ⅱ)若![]() 为
为![]() 轴上异于
轴上异于![]() 的点,且
的点,且![]() ,求点
,求点![]() 横坐标的取值范围.
横坐标的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(Ⅰ)利用三角函数的定义,结合两角和差的余弦公式进行计算即可;(Ⅱ) 若![]() ,则
,则![]() ,设
,设![]() ,可得
,可得![]() ,利用向量垂直的坐标公式,可得
,利用向量垂直的坐标公式,可得![]() ,由
,由![]() ,结合余弦函数的单调性可得结果.
,结合余弦函数的单调性可得结果.
(Ⅰ)∵点A、B纵坐标分别为![]() 、
、![]() ,
,
∴sinα=![]() ,sinβ=
,sinβ=![]() ,
,
∵α为锐角,β为钝角,
![]()
![]()
(Ⅱ)依题意得A(cosα,sinα),B(cosβ,sinβ),
∵AOB=90,即β=α+90,
∴B(-sinα,cosα),
设![]()
∴(-x+cosα)(-x-sinα)+sinα·cosα=0,
整理得x2+x(sinα-cosα)=0,(x0),
∴x=cosα-sinα=![]() cos(α+
cos(α+![]() ),(x0),
),(x0),
![]()
所以x(-1,0)∪(0,1).

练习册系列答案
相关题目

