题目内容
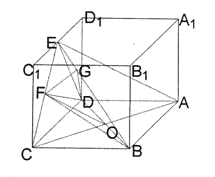
【题目】如图,长方体ABCD﹣A1B1C1D1中,DA=DC=2,![]() ,E是C1D1的中点,F是CE的中点.
,E是C1D1的中点,F是CE的中点.
(1)求证:EA∥平面BDF;
(2)求证:平面BDF⊥平面BCE;
(3)求二面角D﹣EB﹣C的正切值.

【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)连接AC交BD于O点,连接OF,因为OF是△ACE的中位线,则OF∥AE,由线面平行的判定定理得证;
(2)欲证平面BDF⊥平面BCE,找线面垂直,根据线面垂直的判定定理可知DF⊥平面BCE,又DF平面BDF,从而得到结论;
(3)由(2)知DF⊥平面BCE,过F作FG⊥BE于G点,连接DG,则DG在平面BCE中的射影为FG,则∠DGF即为二面角D﹣EB﹣C的平面角,在三角形DGF中求出此角的正切值即可.
(1)连接AC交BD于O点,连接OF,可得OF是△ACE的中位线,OF∥AE,
又AE平面BDF,OF平面BDF,所以EA∥平面BDF;
(2)计算可得DE=DC=2,又F是CE的中点,所以DF⊥CE
又BC⊥平面CDD1C1,所以DF⊥BC,又BC∩CE=C,所以DF⊥平面BCE
又DF平面BDF,所以平面BDF⊥平面BCE;
(3)由(2)知DF⊥平面BCE,过F作FG⊥BE于G点,连接DG,因为DF⊥BE,![]() ,所以
,所以![]() 平面
平面![]() ,从而DG⊥BE,
,从而DG⊥BE,
所以∠DGF即为二面角D﹣EB﹣C的平面角,设其大小为θ,
计算得![]() ,
,![]() ,
,![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目