题目内容
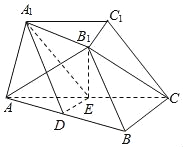
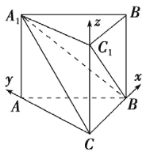
【题目】《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1千多年.在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵,阳马指底面为矩形,一侧棱垂直于底面的四棱锥,鳖臑指四个面均为直角三角形的四面体.如图,在堑堵![]() 中,
中,![]() .
.

(1)求证:四棱锥![]() 为阳马;并判断四面体
为阳马;并判断四面体![]() 是否为鳖臑,若是,请写出各个面的直角(要求写出结论).
是否为鳖臑,若是,请写出各个面的直角(要求写出结论).
(2)若![]() ,当阳马
,当阳马![]() 体积最大时,求二面角
体积最大时,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;是,![]() ,
,![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)由堑堵![]() 的性质得:四边形
的性质得:四边形![]() 是矩形,推导出
是矩形,推导出![]() ,
,![]() ,从而BC⊥平面
,从而BC⊥平面![]() ,由此能证明四棱锥
,由此能证明四棱锥![]() 为阳马,四面体
为阳马,四面体![]() 是否为鳖臑;
是否为鳖臑;
(2)阳马B﹣A1ACC1的体积:阳马![]() 的体积:
的体积:![]()
![]() ,当且仅当
,当且仅当![]() 时,
时,![]() ,以
,以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,利用向量法能求出当阳马
轴,建立空间直角坐标系,利用向量法能求出当阳马![]() 体积最大时,二面角
体积最大时,二面角![]() 的余弦值.
的余弦值.
证明:(1)由堑堵![]() 的性质得:四边形
的性质得:四边形![]() 是矩形,
是矩形,![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
又![]() ,
,![]()
![]() ,
,![]() 平面
平面![]() ,
,![]() 面
面![]() ,
,![]() 四棱锥
四棱锥![]() 为阳马,
为阳马,
四面体![]() 为鳖臑,四个面的直角分别是
为鳖臑,四个面的直角分别是![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)![]() ,由(1)知阳马
,由(1)知阳马![]() 的体积:
的体积:
![]()
![]() ,当且仅当
,当且仅当![]() 时,
时,![]() ,
,
以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,则
轴,建立空间直角坐标系,则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,则
,则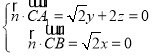 ,取
,取![]() ,得
,得![]() ,
,
设平面![]() 的法向量
的法向量![]() ,则
,则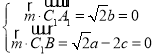 ,取
,取![]() ,得
,得![]() ,
,
设当阳马![]() 体积最大时,二面角
体积最大时,二面角![]() 的平面角为
的平面角为![]() ,则
,则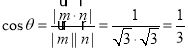 ,
,
当阳马![]() 体积最大时,二面角
体积最大时,二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
相关题目