题目内容
【题目】(A)已知数列![]() 满足
满足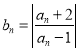 ,其中
,其中![]() ,
, ![]() .
.
(1)求![]() ,
, ![]() ,
, ![]() ,并猜想
,并猜想![]() 的表达式(不必写出证明过程);
的表达式(不必写出证明过程);
(2)由(1)写出数列![]() 的前
的前![]() 项和
项和![]() ,并用数学归纳法证明.
,并用数学归纳法证明.
(B)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
, ![]() .
.
(1)猜想![]() 的表达式,并用数学归纳法证明;
的表达式,并用数学归纳法证明;
(2)设![]() ,
, ![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(A)(1)详见解析;(2)详见解析.(B)(1)详见解析;(2)![]() .
.
【解析】试题分析:(A)(1)利用![]() 的递推关系得到
的递推关系得到![]() ,从而求得
,从而求得![]() ,由此猜想
,由此猜想![]() .(2)由于
.(2)由于![]() 是等比数列,利用前
是等比数列,利用前![]() 项和公式可得
项和公式可得![]() 的表达式,然后利用数学归纳法的证明过程证明结论. (B)(1)利用
的表达式,然后利用数学归纳法的证明过程证明结论. (B)(1)利用![]() ,和
,和![]() 的递推关系,可求得
的递推关系,可求得![]() 的值,由此猜想
的值,由此猜想![]() .然后利用数学归纳法的证明过程证明结论. (2)利用
.然后利用数学归纳法的证明过程证明结论. (2)利用![]() ,可求得
,可求得![]() 的通项公式,代入
的通项公式,代入![]() 并化简,利用函数的单调性可求得其最大值.
并化简,利用函数的单调性可求得其最大值.
试题解析:
(A)解(1)由题意, ![]() ,
, ![]() ,
, ![]() ,
,
则![]() ,
, ![]() ,
, ![]() ,
,
猜想得: ![]() .
.
(2)由(1),数列![]() 是以4为首项,公比为2的等比数列,
是以4为首项,公比为2的等比数列,
则有![]() ,
,
证明:当![]() 时,
时, ![]() 成立,
成立,
假设当![]() 时,有
时,有![]() ,
,
则当![]() 时,
时, ![]() ,
,
综上有![]() 成立.
成立.
(B)(1)![]() ,
,
由![]() ,得
,得![]() ,
,
由![]() ,得
,得![]() ,
,
猜想得: ![]() ,
,
证明:当![]() 时,
时, ![]() 成立,
成立,
假设当![]() 时,有
时,有![]() ,
,
则当![]() 时,
时, ![]() ,
, 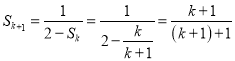 .
.
综上, ![]() 成立.
成立.
(2)由(1),![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() 满足止式,
满足止式,
所以![]() ,则
,则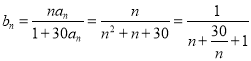 ,
, ![]() ,
,
设![]() ,则有
,则有![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,因为
上为增函数,因为![]() ,且
,且![]() ,所以当
,所以当![]() 或
或![]() 时,
时, ![]() 有最大值
有最大值![]() .
.

练习册系列答案
相关题目