题目内容

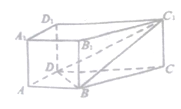
【题目】在四棱锥中， 平面，底面为矩形， ，该四棱锥的外接球的体积为，则到平面的距离为（ ）

A. B. C. D.

【答案】C

【解析】 得出，外接球的球心O在底面中心E的正上方，且

OE=PD，在直角三角形OEA中，AE=4，R=5，所以OE=3，则PD=6，因为AD平行于面PBC，所以点到平面的距离与点D到平面的距离相等，取点M做DM⊥PC，∵PD⊥面ABCD，∴PD⊥BC，又BC⊥CD，PD∩CD=D，∴BC⊥面PDC，又BC面PBC，∴面PBC⊥面PDC，PC为交线，又在直角△PDC中，有DM⊥PC，∴DM⊥面PBC，∴DM即为所求距离，在Rt△PDC中，PD=6，DC=，故DM=，

即点D到平面PBC的距离等于，则到平面的距离为.

练习册系列答案
相关题目

【题目】设函数， = .

（Ⅰ）求函数的单调区间；

（Ⅱ）若函数有两个零点.

(1)求满足条件的最小正整数的值；

(2)求证： .

【题目】已知函数， .

（Ⅰ）证明： ，直线都不是曲线的切线；

（Ⅱ）若，使成立，求实数的取值范围.

【题目】有下列四个命题

①“若，则互为相反数”的逆命题；

②“全等三角形的面积相等”的否命题；

③“若，则有实根”的逆否命题；

④“不等边三角形的三个内角相等”的逆命题.

其中真命题为_______________.

【题目】如图，四棱柱中，底面，底面是梯形，，，.

（1）求证：平面平面；

（2）在线段上是否存在一点，使平面，若存在，请确定点的位置；若不存在，请说明理由.

【题目】设m，n是两条不同的直线，α，β是两个不同的平面，则下列叙述正确的是（ ）
A.若α∥β，m∥α，n∥β，则m∥n
B.若α⊥β，m⊥α，n∥β，则m⊥n
C.若m∥α，n∥α，m∥β，n∥β，m⊥n，则α∥β
D.若m⊥α，nβ，m⊥n，则α⊥β

【题目】如图，三棱柱中， 是正三角形，四边形是矩形，且.

（1）求证:平面平面；

（2）若点在线段上，且，当三棱锥的体积为时，求实数的值.

【题目】

一个盒子里装有三张卡片，分别标记有数字1,2,3，这三张卡片除标记的数字外完全相同.随机有放回地抽取3次，每次抽取1张，将抽取的卡片上的数字依次记为.

（1）求“抽取的卡片上的数字满足”的概率；

（2）求“抽取的卡片上的数字不完全相同”的概率.

【题目】某折叠餐桌的使用步骤如图所示，有如图检查项目：

项目①：折叠状态下（如图1），检查四条桌腿长相等；

项目②：打开过程中（如图2），检查；

项目③：打开过程中（如图2），检查；

项目④：打开后（如图3），检查；

项目⑤：打开后（如图3），检查．

在检查项目的组合中，可以正确判断“桌子打开之后桌面与地面平行的是”（ ）

A. ①②③ B. ②③④ C. ②④⑤ D. ③④⑤

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网