题目内容
【题目】已知数列{an}的前n项和为Sn , 且Sn=2an﹣3n(n∈N+).
(1)求a1 , a2 , a3的值;
(2)设bn=an+3,证明数列{bn}为等比数列,并求通项公式an .
【答案】
(1)解:∵数列{an}的前n项和为Sn,且Sn=2an﹣3n(n∈N+).
∴n=1时,由a1=S1=2a1﹣3×1,解得a1=3,
n=2时,由S2=2a2﹣3×2,得a2=9,
n=3时,由S3=2a3﹣3×3,得a3=21.
(2)解:∵Sn=2an﹣3×n,∴Sn+1=2an+1﹣3×(n+1),
两式相减,得an+1=2an+3,*
把bn=an+3及bn+1=an+1+3,代入*式,
得bn+1=2bn,(n∈N*),且b1=6,
∴数列{bn}是以6为首项,2为公比的等比数列,
∴bn=6×2n﹣1,
∴ ![]() .
.
【解析】(1)根据递推公式Sn=2an﹣3n,可求出所求值,(2)由Sn=2an﹣3×n,则Sn+1=2an+1﹣3×(n+1),两式相减得an+1=2an+3,将bn代入可得bn+1=2bn,数列{bn}是以6为首项,2为公比的等比数列bn=6×2n﹣1,a n = b n 3= 3 ( 2 n 1 ) .
【考点精析】利用等比数列的通项公式(及其变式)和数列的前n项和对题目进行判断即可得到答案,需要熟知通项公式:![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系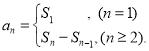 .
.

练习册系列答案
相关题目