题目内容
 (2013•汕头一模)如图.已知椭圆
(2013•汕头一模)如图.已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| AF1 |
| F1B |
(I)求椭圆的标准方程;
(II)设P是椭圆上异于A、B的任意一点,PH⊥x轴,H为垂足,延长HP到点Q使得HP=PQ.连接AQ并延长交直线l于点M,N为MB的中点,判定直线QN与以AB为直径的圆O的位置关系.
分析:(I)写出A,B,F1的坐标,进而得到
,
的坐标,代入
•
=1并化简得b2=1,由e=
,得e2=
=
=
,解出得a2,从而得椭圆方程;
(II)可根据圆心O到直线QN的距离d与圆的半径的大小关系判断:设P(x0,y0),则Q(x0,2y0)(x0≠±2),由点斜式写出直线AQ方程,与直线BM方程联立可得M坐标,进而得N点坐标,由点斜式可得直线QN方程,根据点到直线距离公式可得圆心O到直线QN的距离,与半径a比较即可,注意点P坐标满足椭圆方程;
| AF1 |
| F1B |
| AF1 |
| F1B |
| ||
| 2 |
| c2 |
| a2 |
| a2-1 |
| a2 |
| 3 |
| 4 |
(II)可根据圆心O到直线QN的距离d与圆的半径的大小关系判断:设P(x0,y0),则Q(x0,2y0)(x0≠±2),由点斜式写出直线AQ方程,与直线BM方程联立可得M坐标,进而得N点坐标,由点斜式可得直线QN方程,根据点到直线距离公式可得圆心O到直线QN的距离,与半径a比较即可,注意点P坐标满足椭圆方程;
解答: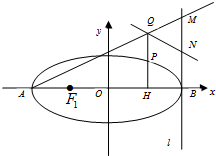 解:(Ⅰ)易知A(-a,0),B(a,0),F1(-c,0),
解:(Ⅰ)易知A(-a,0),B(a,0),F1(-c,0),
∴
•
=(a-c,0)•(a+c)=1,∴a2-c2=b2=1,
又e=
,∴e2=
=
=
,解得a2=4,
∴所求椭圆方程为:
+y2=1;
(Ⅱ)设P(x0,y0),则Q(x0,2y0)(x0≠±2),
∴kAQ=
,所以直线AQ方程:y=
(x+2),
∴M(2,
),则N(2,
),
∴kQN=
=
,
又点P的坐标满足椭圆方程,则x02+4y02=4,
所以 x02-4=-4y02,∴kQN=
=
=-
,
∴直线QN的方程:y-2y0=-
(x-x0),
化简整理得到:x0x+2y0y=x02+4y02=4,即x0x+2y0y=4,
所以点O到直线QN的距离d=
=2,
故直线QN与AB为直径的圆O相切.
 解:(Ⅰ)易知A(-a,0),B(a,0),F1(-c,0),
解:(Ⅰ)易知A(-a,0),B(a,0),F1(-c,0),∴
| AF1 |
| F1B |
又e=
| ||
| 2 |
| c2 |
| a2 |
| a2-1 |
| a2 |
| 3 |
| 4 |
∴所求椭圆方程为:
| x2 |
| 4 |
(Ⅱ)设P(x0,y0),则Q(x0,2y0)(x0≠±2),
∴kAQ=
| 2y0 |
| x0+2 |
| 2y0 |
| x0+2 |
∴M(2,
| 8y0 |
| x0+2 |
| 4y0 |
| x0+2 |
∴kQN=
| ||
| 2-x0 |
| 2x0y0 |
| x02-4 |
又点P的坐标满足椭圆方程,则x02+4y02=4,
所以 x02-4=-4y02,∴kQN=
| 2x0y0 |
| x02-4 |
| 2x0y0 |
| -4y02 |
| x0 |
| 2y0 |
∴直线QN的方程:y-2y0=-
| x0 |
| 2y0 |
化简整理得到:x0x+2y0y=x02+4y02=4,即x0x+2y0y=4,
所以点O到直线QN的距离d=
| 4 | ||
|
故直线QN与AB为直径的圆O相切.
点评:本题考查直线、椭圆方程及其位置关系,考查学生的运算能力,本题中动点较多,设点坐标时应尽量减少未知量的个数.

练习册系列答案
相关题目