题目内容
(2013•汕头一模)已知函数f(x)=x2-lnx.
(1)求曲线f(x)在点(1,f(1))处的切线方程;
(2)求函数f(x)的单调递减区间:
(3)设函数g(x)=f(x)-x2+ax,a>0,若x∈(O,e]时,g(x)的最小值是3,求实数a的值.(e是为自然对数的底数)
(1)求曲线f(x)在点(1,f(1))处的切线方程;
(2)求函数f(x)的单调递减区间:
(3)设函数g(x)=f(x)-x2+ax,a>0,若x∈(O,e]时,g(x)的最小值是3,求实数a的值.(e是为自然对数的底数)
分析:(1)欲求在点(1,f(1))处的切线方程,只须求出其斜率的值即可,故先利用导数求出在x=1处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决.
(2)求出原函数的导函数,由导函数小于0求出自变量x在定义域内的取值范围,则原函数的单调减区间可求.
(3)求导函数,分类讨论,确定函数的单调性,利用函数g(x)的最小值是3,即可求出a的值.
(2)求出原函数的导函数,由导函数小于0求出自变量x在定义域内的取值范围,则原函数的单调减区间可求.
(3)求导函数,分类讨论,确定函数的单调性,利用函数g(x)的最小值是3,即可求出a的值.
解答:解:(1)∵f(x)=x2-lnx
∴f′(x)=2x-
.
∴f'(1)=1.
又∵f(1)=1,
∴曲线y=f(x)在点(1,f(1))处的切线方程为y-1=x-1.即x-y=0.
(2)因为函数f(x)=2x2-lnx的定义域为(0,+∞),
由f′(x)=2x-
<0,得0<x<
.
所以函数f(x)=x2-lnx的单调递减区间是(0,
).
(3)∵g(x)=ax-lnx,∴g′(x)=
,令g′(x)=0,得x=
,
①当
≥e时,即0<a≤
时,g′(x)=
≤0在(0,e]上恒成立,
则g(x)在(0,e]上单调递减,g(x)min=g(e)=ae-1=3,a=
(舍去),
②当0<
<e时,即a>
时,列表如下:
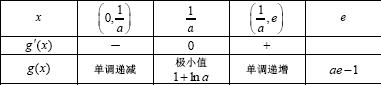
由表知,g(x)min=g(
)=1+lna=3,a=e2,满足条件.
综上,所求实数a=e2,使得当x∈(0,e]时g(x)有最小值3.
∴f′(x)=2x-
| 1 |
| x |
∴f'(1)=1.
又∵f(1)=1,
∴曲线y=f(x)在点(1,f(1))处的切线方程为y-1=x-1.即x-y=0.
(2)因为函数f(x)=2x2-lnx的定义域为(0,+∞),
由f′(x)=2x-
| 1 |
| x |
| ||
| 2 |
所以函数f(x)=x2-lnx的单调递减区间是(0,
| ||
| 2 |
(3)∵g(x)=ax-lnx,∴g′(x)=
| ax-1 |
| x |
| 1 |
| a |
①当
| 1 |
| a |
| 1 |
| e |
| ax-1 |
| x |
则g(x)在(0,e]上单调递减,g(x)min=g(e)=ae-1=3,a=
| 4 |
| e |
②当0<
| 1 |
| a |
| 1 |
| e |

由表知,g(x)min=g(
| 1 |
| a |
综上,所求实数a=e2,使得当x∈(0,e]时g(x)有最小值3.
点评:本小题主要考查直线的斜率、导数的几何意义、利用导数研究曲线上某点切线方程,考查导函数的正负与原函数的单调性之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减,是中档题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目