题目内容
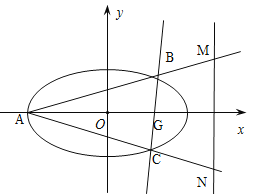
【题目】已知![]() 为椭圆
为椭圆![]() 上的三个点,
上的三个点,![]() 为坐标原点.
为坐标原点.
(1)若![]() 所在的直线方程为
所在的直线方程为![]() ,求
,求![]() 的长;
的长;
(2)设![]() 为线段
为线段![]() 上一点,且
上一点,且![]() ,当
,当![]() 中点恰为点
中点恰为点![]() 时,判断
时,判断![]() 的面积是否为常数,并说明理由.
的面积是否为常数,并说明理由.
【答案】(1)![]() ;(2)定值为
;(2)定值为![]()
【解析】
试题(1)因为求![]() 所在的直线方程为
所在的直线方程为![]() 与椭圆方程
与椭圆方程![]() 相交所得的弦长.一般是通过联立两方程,消去y,得到关于x的一元二次方程,可以解得两个交点的坐标的横坐标,确定点的坐标,从而根据两点的距离公式求出弦长.
相交所得的弦长.一般是通过联立两方程,消去y,得到关于x的一元二次方程,可以解得两个交点的坐标的横坐标,确定点的坐标,从而根据两点的距离公式求出弦长.
(2)直线与圆的位置关系,首先考虑直线的斜率是否存在,做好分类的工作.若当斜率存在时,通过联立方程,应用韦达定理知识,求出弦长,利用点到直线的距离公式求出三角形的高的长.从而写出三角形的面积(含斜率的等式).再根据![]() 的关系求出点P的坐标,带到椭圆方程中,即可求出含斜率的一个等式,从而可得结论.
的关系求出点P的坐标,带到椭圆方程中,即可求出含斜率的一个等式,从而可得结论.
试题解析:(1)由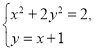 得
得![]() ,
,
解得![]() 或
或![]() ,
,
所以![]() 两点的坐标为
两点的坐标为![]() 和
和![]() 所以
所以![]() .
.
(2)①若![]() 是椭圆的右顶点(左顶点一样),则
是椭圆的右顶点(左顶点一样),则![]() ,
,
因为![]() ,
,![]() 在线段
在线段![]() 上,所以
上,所以![]() ,求得
,求得![]() ,
,
所以![]() 的面积等于
的面积等于![]() .
.
②若B不是椭圆的左、右顶点,设![]() ,
,![]() ,
,
由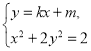 得
得![]()
![]() ,
,![]() ,
,
所以,![]() 的中点
的中点![]() 的坐标为
的坐标为![]() ,
,
所以![]() ,代入椭圆方程,化简得
,代入椭圆方程,化简得![]() .
.
计算![]()
![]()
![]()
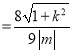 .
.
因为点![]() 到
到![]() 的距离
的距离![]()
![]()
所以,![]() 的面积
的面积![]()
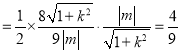 .
.
综上,![]() 面积为常数
面积为常数![]() .
.

练习册系列答案
相关题目