题目内容
7.已知C,D是圆A:(x+1)2+y2=1与圆B:x2+(y-2)2=4的公共点,则△BCD的面积为( )| A. | 4545 | B. | 8585 | C. | 4√554√55 | D. | 8√558√55 |
分析 求出公共弦方程,B到CD的距离,CD的距离,然后求解面积.
解答 解:C,D是圆A:(x+1)2+y2=1与圆B:x2+(y-2)2=4的公共点,
可得CD的方程为:2x+4y=0,即x+2y=0,
圆B:x2+(y-2)2=4的圆心(0,2),半径为2,
B到CD的距离为:4√12+224√12+22=4√54√5,|CD|=2√22−(4√5)2=4√5.
△BCD的面积为:12×4√5×4√5=85.
故选:B.
点评 本题考查圆与圆的位置关系的应用,点到直线的距离以及三角形的面积的求法,考查计算能力.

练习册系列答案
相关题目
18.用辗转相除法求294和84的最大公约数,则所求最大公约数为 ( )
| A. | 21 | B. | 42 | C. | 84 | D. | 168 |
2.设p,q是两个命题,则“p,q均为假命题”是“p∧q为假命题”的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充分必要 | D. | 既不充分也不必要 |
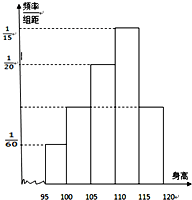 某幼儿园中班共36个小朋友的身高(单位:厘米)测量结果如下频率
某幼儿园中班共36个小朋友的身高(单位:厘米)测量结果如下频率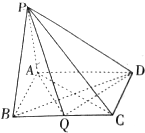 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=aBC(a>0).
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=aBC(a>0).