题目内容
【题目】如图,已知![]() 是正三角形,EA,CD都垂直于平面ABC,且
是正三角形,EA,CD都垂直于平面ABC,且![]() ,二面角
,二面角![]() 的平面角大小为
的平面角大小为![]() ,F是BE的中点,求证:
,F是BE的中点,求证:
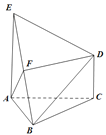
(1)![]() 平面ABC;
平面ABC;
(2)![]() 平面EDB;
平面EDB;
(3)求几何体![]() 的体积.
的体积.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)取BA的中点M,连结CM,通过证明四边形FMCD是平行四边形,证得![]() ,从而证得结论;
,从而证得结论;
(2)先证![]() 面EAB,
面EAB,![]() ,得到
,得到![]() ,再由已知可得
,再由已知可得![]() ,即可得出结论;
,即可得出结论;
(3)几何体![]() 为四棱锥
为四棱锥![]() ,取AC中点N,连接BN,可证
,取AC中点N,连接BN,可证![]() 平面ACDE,即可求出体积.
平面ACDE,即可求出体积.
(1)![]() 平面ABC,
平面ABC,![]() ,
,
取BA的中点M,连结CM,DM,
![]() ,
,![]() 平面
平面![]() ,
,
![]() 为二面角
为二面角![]() 的平面角,
的平面角,
所以![]() ,
,
∵![]() ,
,![]() ,则
,则![]() .
.
∵F,M分别是BE,AB的中点,
∴![]() ,
,![]()
∵EA、CD都垂直于平面ABC,∴![]() ,
,
∴![]() ,又
,又![]()
∴四边形FMCD是平行四边形,∴![]() ,
,
![]() 平面ABC,
平面ABC,![]() 平面ABC,∴
平面ABC,∴![]() 平面ABC.
平面ABC.
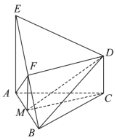
(2)因M是AB的中点,![]() 是正三角形,所以
是正三角形,所以![]()
又EA垂直于平面ABC∴![]() ,
,
又![]() ,所以
,所以![]() 面EAB,∵
面EAB,∵![]() 面EAB
面EAB
∴![]() ,又
,又![]() ,从而
,从而![]() ,
,
因F是BE的中点,![]() 所以
所以![]() .
.
EB,FD是平面EDB内两条相交直线,所以![]() 平面EDB.
平面EDB.
(3)几何体![]() 的体积等于
的体积等于![]()
N为AC中点,连接BN
![]() ,
,![]() 平面ACDE
平面ACDE
![]() ,
,
所以几何体![]() 的体积为
的体积为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某校为提高课堂教学效果,最近立项了市级课题《高效课堂教学模式及其运用》,其中王老师是该课题的主研人之一,为获得第一手数据,她分别在甲、乙两个平行班采用“传统教学”和“高效课堂”两种不同的教学模式进行教学实验.为了解教改实效,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出如图所示的茎叶图,成绩大于70分为“成绩优良”.
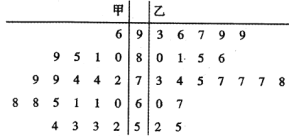
(1)由以上统计数据填写下面![]() 列联表,并判断能否在犯错误的概率不超过
列联表,并判断能否在犯错误的概率不超过![]() 的前提下认为“成绩优良与教学方式有关”?
的前提下认为“成绩优良与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总计 |
(2)从甲、乙两班40个样本中,成绩在60分以下(不含60分)的学生中任意选取2人,记来自甲班的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
附: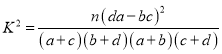 (其中
(其中![]() )
)
|
|
|
|
|
|
|
|
|
|