题目内容
【题目】已知
和
个实数
若有穷数列
由数列
的项重新排列而成,且下列条件同时成立：① 
个数
两两不同；②当
时，
都成立，则称为的一个“友数列”.
(1)若
写出的全部“友数列”；
(2)已知是通项公式为
的数列的一个“友数列”，且
求
(用
表示)；
(3)设
求所有使得通项公式为
的数列不能成为任何数列的“友数列”的正实数
的个数(用表示).
【答案】（1）见解析（2）见解析（3）见解析
【解析】
（1）对
分类讨论即可得到结果；
（2）由条件①知：3n个数两两不同，又
，
，∴差值最大为3n，分类讨论即可得到结果；
（3）根据“友数列”的定义，分析即可得到结果.
解：（1）若
则
中存在两个1，不妨设
，
则有
与②矛盾，
故有
则
，
∴
∴
即好数列
；
（2）由条件①知：3n个数两两不同，又 ，
，
∴差值最大为3n，
而令k取1时，由
，
，
若
，则
，
而
时，
故只可能为某个
且
使
，
则
，矛盾，
∴必有
则有
，即
，
其次，若
则此时差值中
除
外最大，
则有
，，又
，
∴
，而
，
则
矛盾，
∴必有
即
同理，若
则有使
，且
，
且，∴
矛盾，
∴必有
即
，
接着考虑：
，
，
若
，
则有
，使得
，
又
，
矛盾，
∴
依次类推即可.
故对于
时，
且
，
，
，
联立，得
，
∴
，
对于
时，
，
，
，
联立，得
，
∴
，
（3）
，
若
为一个数列
的“友数列”，
则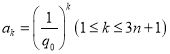
亦为一个数列
的友数列，
故不妨设
，则所有差排列如下：
：
时，易知与条件①②矛盾；
：
时，
，
，
观察上面式子，若不存在，则先比较：
与
，
，
在比较
与
大小，
，
综上，不存在满足题意的q值.
练习册系列答案
相关题目
