ĢāÄæÄŚČŻ
”¾ĢāÄæ”æijŠ£ĪŖĢįøßæĪĢĆ½ĢѧŠ§¹ū£¬×ī½üĮ¢ĻīĮĖŹŠ¼¶æĪĢā”¶øߊ§æĪĢĆ½ĢŃ§Ä£Ź½¼°ĘäŌĖÓĆ”·£¬ĘäÖŠĶõĄĻŹ¦ŹĒøĆæĪĢāµÄÖ÷ŃŠČĖÖ®Ņ»£¬ĪŖ»ńµĆµŚŅ»ŹÖŹż¾Ż£¬Ėż·Ö±šŌŚ¼×”¢ŅŅĮ½øöĘ½ŠŠ°ą²ÉÓĆ”°“«Ķ³½Ģѧ”±ŗĶ”°øߊ§æĪĢĆ”±Į½ÖÖ²»Ķ¬µÄ½ĢŃ§Ä£Ź½½ųŠŠ½ĢѧŹµŃé.ĪŖĮĖ½ā½ĢøÄŹµŠ§£¬ĘŚÖŠæ¼ŹŌŗ󣬷ֱš“ÓĮ½øö°ą¼¶ÖŠø÷Ė껜³éČ”20ĆūѧɜµÄ³É¼Ø½ųŠŠĶ³¼Ę£¬×÷³öČēĶ¼ĖłŹ¾µÄ¾„Ņ¶Ķ¼£¬³É¼Ø“óÓŚ70·ÖĪŖ”°³É¼ØÓÅĮ¼”±.
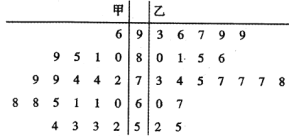
£Ø1£©ÓÉŅŌÉĻĶ³¼ĘŹż¾ŻĢīŠ“ĻĀĆę![]() ĮŠĮŖ±ķ£¬²¢ÅŠ¶ĻÄÜ·ńŌŚ·ø“ķĪóµÄøÅĀŹ²»³¬¹ż
ĮŠĮŖ±ķ£¬²¢ÅŠ¶ĻÄÜ·ńŌŚ·ø“ķĪóµÄøÅĀŹ²»³¬¹ż![]() µÄĒ°ĢįĻĀČĻĪŖ”°³É¼ØÓÅĮ¼Óė½Ģѧ·½Ź½ÓŠ¹Ų”±£æ
µÄĒ°ĢįĻĀČĻĪŖ”°³É¼ØÓÅĮ¼Óė½Ģѧ·½Ź½ÓŠ¹Ų”±£æ
¼×°ą | ŅŅ°ą | ×Ü¼Ę | |
³É¼ØÓÅĮ¼ | |||
³É¼Ø²»ÓÅĮ¼ | |||
×Ü¼Ę |
£Ø2£©“Ó¼×”¢ŅŅĮ½°ą40øöŃł±¾ÖŠ£¬³É¼ØŌŚ60·ÖŅŌĻĀ£Ø²»ŗ¬60·Ö£©µÄѧɜ֊ČĪŅāєȔ2ČĖ£¬¼ĒĄ“×Ō¼×°ąµÄČĖŹżĪŖ![]() £¬Ēó
£¬Ēó![]() µÄ·Ö²¼ĮŠÓėŹżŃ§ĘŚĶū.
µÄ·Ö²¼ĮŠÓėŹżŃ§ĘŚĶū.
ø½£ŗ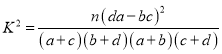 £ØĘäÖŠ
£ØĘäÖŠ![]() £©
£©
|
|
|
|
|
|
|
|
|
|
”¾“š°ø”æ£Ø1£©ĮŠĮŖ±ķ¼ū½āĪö£¬ÄÜŌŚ·ø“ķĪóµÄøÅĀŹ²»³¬¹ż0.05µÄĒ°ĢįĻĀČĻĪŖ”°³É¼ØÓÅĮ¼Óė½Ģѧ·½Ź½ÓŠ¹Ų”±£»£Ø2£©·Ö²¼ĮŠ¼ū½āĪö£¬![]() .
.
”¾½āĪö”æ
(1)øł¾Ż¾„Ņ¶Ķ¼ÖŠµÄŹż¾ŻĢīŠ“ĮŠĮŖ±ķ,Č»ŗó¼ĘĖć![]() ,ŌŁ¶ŌÕÕ±ķµĆ³ö½įĀŪ;
,ŌŁ¶ŌÕÕ±ķµĆ³ö½įĀŪ;
(2)ĻČČ·¶Ø¼×°ąČĖŹż![]() µÄĖłÓŠæÉÄÜȔֵ,Č»ŗó·Ö±šĒóĘäøÅĀŹ,ŌŁµĆµ½XµÄ·Ö²¼ĮŠŗĶŹżŃ§ĘŚĶū.
µÄĖłÓŠæÉÄÜȔֵ,Č»ŗó·Ö±šĒóĘäøÅĀŹ,ŌŁµĆµ½XµÄ·Ö²¼ĮŠŗĶŹżŃ§ĘŚĶū.
½ā:(1)øł¾Ż¾„Ņ¶Ķ¼ÖŠµÄŹż¾Ż×÷³ö![]() ĮŠĮŖ±ķČē±ķĖłŹ¾,
ĮŠĮŖ±ķČē±ķĖłŹ¾,
¼×°ą | ŅŅ°ą | ×Ü¼Ę | |
³É¼ØÓÅĮ¼ | 10 | 16 | 26 |
³É¼Ø²»ÓÅĮ¼ | 10 | 4 | 14 |
×Ü¼Ę | 20 | 20 | 40 |
øł¾Ż![]() ĮŠĮŖ±ķÖŠµÄŹż¾Ż,µĆ
ĮŠĮŖ±ķÖŠµÄŹż¾Ż,µĆ![]() ,
,
ĖłŅŌÄÜŌŚ·ø“ķĪóµÄøÅĀŹ²»³¬¹ż0.05µÄĒ°ĢįĻĀČĻĪŖ”°³É¼ØÓÅĮ¼Óė½Ģѧ·½Ź½ÓŠ¹Ų”±.
(2)¼×”¢ŅŅĮ½°ą40øöŃł±¾ÖŠ,³É¼ØŌŚ60·ÖŅŌĻĀ(²»ŗ¬60·Ö)µÄѧɜČĖŹżĪŖ6.
ÓÉĢāŅāæÉÖŖXµÄȔֵ·Ö±šĪŖ![]() ,
,![]() ,
,![]() ,Ōņ
,Ōņ
![]() £»
£»![]() £»
£»![]() .
.
”ą![]() µÄ·Ö²¼ĮŠĪŖ
µÄ·Ö²¼ĮŠĪŖ
| 0 | 1 | 2 |
|
|
|
|
Ę䏿ѧʌĶū![]()
![]() .
.