题目内容
已知关于x的二次函数f(x)=ax2-4bx+1.设集合P={-1,1,2,3,4,5},集合Q={-2,-1,1,2,3,4},分别从集合P和Q中任取一个数作为a和b的值,求函数y=f(x)在区间[1,+∞)上是增函数的概率.
二次函数f(x)=ax2-4bx+1图象的对称轴为x=
.要使y=f(x)在区间[1,+∞)上为增函数,应有a>0且
≤1,∴a≥2b,且a>0.(3分)
①若a=1,则b=-2,-1;
②若a=2,则b=-2,-1,1;
③若a=3,则b=-2,-1,1;
④若a=4,则b=-2,-1,1,2;
⑤若a=5,则b=-2,-1,1,2,(9分)
∴故满足条件的数对(a,b)共有16个,而所有的数对(a,b)有6×6=36个,
∴所求概率P=
=
.(12分)
| 2b |
| a |
| 2b |
| a |
①若a=1,则b=-2,-1;
②若a=2,则b=-2,-1,1;
③若a=3,则b=-2,-1,1;
④若a=4,则b=-2,-1,1,2;
⑤若a=5,则b=-2,-1,1,2,(9分)
∴故满足条件的数对(a,b)共有16个,而所有的数对(a,b)有6×6=36个,
∴所求概率P=
| 16 |
| 6×6 |
| 4 |
| 9 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,再由乙猜甲刚才所想的数字,把乙猜的数字记为
,再由乙猜甲刚才所想的数字,把乙猜的数字记为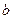 ,其中
,其中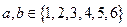 ,若
,若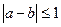 ,就称甲乙“心有灵犀”.现任意找两人玩这个游戏,则他们“心有灵犀”的概率为
,就称甲乙“心有灵犀”.现任意找两人玩这个游戏,则他们“心有灵犀”的概率为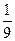 B.
B.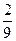 C.
C. D.
D.
 B的非空集合A、B的四个命题中正确的个数是
B的非空集合A、B的四个命题中正确的个数是 ①若任取x∈A,则x∈B是必然事件 ②若x
①若任取x∈A,则x∈B是必然事件 ②若x A,则x∈B是 ③若任取x∈B,则x∈A是随机事件 ④若x
A,则x∈B是 ③若任取x∈B,则x∈A是随机事件 ④若x 张卡片上分别写有数字
张卡片上分别写有数字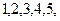 然后将它们混合,再任意排列成一行,则得到的数能被
然后将它们混合,再任意排列成一行,则得到的数能被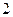 或
或