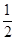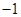题目内容
对于函数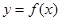 ,存在区间
,存在区间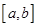 ,当
,当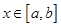 时,
时,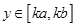
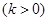 ,则称
,则称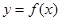 为
为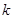 倍值函数。已知
倍值函数。已知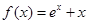 是
是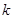 倍值函数,则实数
倍值函数,则实数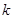 的取值范围是 .
的取值范围是 .
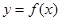 ,存在区间
,存在区间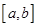 ,当
,当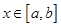 时,
时,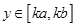
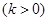 ,则称
,则称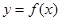 为
为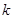 倍值函数。已知
倍值函数。已知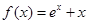 是
是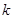 倍值函数,则实数
倍值函数,则实数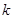 的取值范围是 .
的取值范围是 . 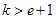
根据新的定义可知当变量给定时,那么对应的值域就是确定的,并且最大值和最小值时自变量的最大值和最小值的k倍,那么根据这一点设出函数求解导数,并分析单调性得到实数k的范围是k>e+1.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
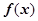 定义域为
定义域为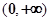 ,且满足
,且满足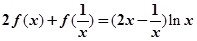 .
.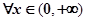 ,
,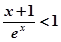 。
。 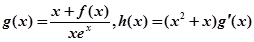 。求证:
。求证: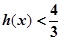 .
.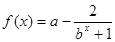
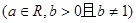
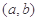 ,
,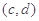 都是函数
都是函数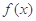 的单调增区间,且
的单调增区间,且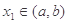 ,
,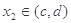 ,若
,若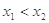 ,则
,则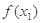 与
与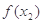 的大小关系是( )
的大小关系是( )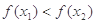
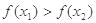
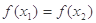
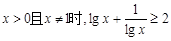
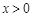 ,
,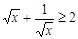
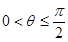 ,
,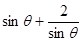 的最小值为
的最小值为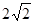
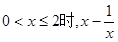 无最大值
无最大值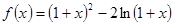 .(1)求
.(1)求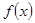 的单调区间;(2)当
的单调区间;(2)当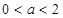 时,求函数
时,求函数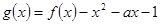 在区间
在区间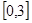 上的最小值.
上的最小值.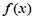 在
在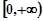 上为增函数,若不等式
上为增函数,若不等式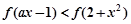 恒成立,则实数
恒成立,则实数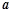 的取值范围为( )
的取值范围为( )
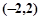
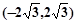

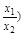 +f(x2)=f(x1),且当x>1时,f(x)<0.
+f(x2)=f(x1),且当x>1时,f(x)<0. 在
在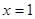 处取到极值,则
处取到极值,则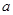 的值为 ( )
的值为 ( )