题目内容
对于函数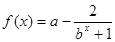
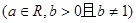
(1)判断函数的单调性并证明; (2)是否存在实数a使函数f (x)为奇函数?并说明理由.
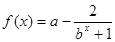
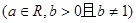
(1)判断函数的单调性并证明; (2)是否存在实数a使函数f (x)为奇函数?并说明理由.
(1)见解析 (2) 故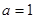 时函数f (x)为奇函数
时函数f (x)为奇函数
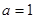 时函数f (x)为奇函数
时函数f (x)为奇函数(1)利用单调性的定义证明:先从定义域R内任取两个不同的值x1 , x2,设设x1 < x2 ,然后再确定 f (x1) – f (x2)的符号,若是正值,是增函数,若是负值是减函数.因为含有参数b,可能要对b进行讨论.
解:(1)函数f (x)的定义域是R ……2分
证明:设x1 < x2;
f (x1) – f (x2) = a-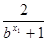 -( a-
-( a-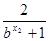 )=
)=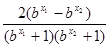
当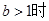
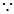 x1<x2
x1<x2 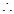
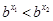 得
得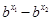 < 0
< 0
得f (x1) – f (x2) < 0所以f (x1) < f (x2)
故此时函数f (x)在R上是单调增函数; ……6分
当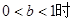
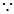 x1<x2
x1<x2 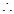
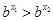 得
得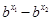
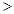 0
0
得f (x1) – f (x2)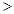 0所以f (x1)
0所以f (x1) 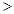 f (x2)
f (x2)
故此时函数f (x)在R上是单调减函数 ……10分
注:用求导法也可证明.
(2) f (x)的定义域是R,
由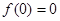 ,求得
,求得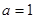 . …11分
. …11分
当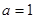 时,
时,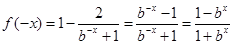 ,
,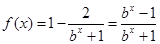 ,
,
满足条件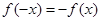 ,故
,故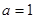 时函数f (x)为奇函数 …14分
时函数f (x)为奇函数 …14分
解:(1)函数f (x)的定义域是R ……2分
证明:设x1 < x2;
f (x1) – f (x2) = a-
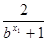 -( a-
-( a-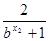 )=
)=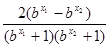
当
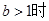
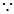 x1<x2
x1<x2 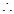
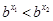 得
得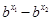 < 0
< 0得f (x1) – f (x2) < 0所以f (x1) < f (x2)
故此时函数f (x)在R上是单调增函数; ……6分
当
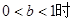
 x1<x2
x1<x2 
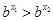 得
得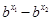
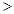 0
0得f (x1) – f (x2)
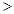 0所以f (x1)
0所以f (x1) 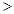 f (x2)
f (x2)故此时函数f (x)在R上是单调减函数 ……10分
注:用求导法也可证明.
(2) f (x)的定义域是R,
由
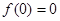 ,求得
,求得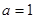 . …11分
. …11分当
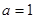 时,
时,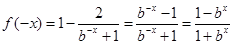 ,
,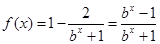 ,
,满足条件
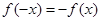 ,故
,故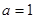 时函数f (x)为奇函数 …14分
时函数f (x)为奇函数 …14分
练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
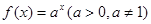 在
在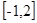 上的最大值为4,最小值为
上的最大值为4,最小值为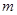 ,且函数
,且函数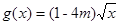 在
在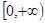 上是增函数,则
上是增函数,则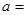 。
。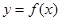 ,存在区间
,存在区间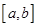 ,当
,当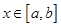 时,
时,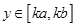
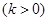 ,则称
,则称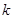 倍值函数。已知
倍值函数。已知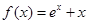 是
是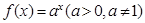 在[-1,2]上的最大值为4,最小值为m,且函数
在[-1,2]上的最大值为4,最小值为m,且函数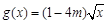 在
在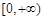 上是增函数,则a= .
上是增函数,则a= .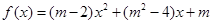 是偶函数,
是偶函数,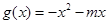 在
在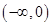 内单调递增,则实数
内单调递增,则实数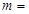 ( )
( )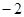
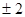
 则满足f(x)≤2的x的取值范围是( )
则满足f(x)≤2的x的取值范围是( )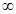 )
)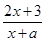 在(-1,+∞)上满足对任意x1<x2,都有f(x1)>f(x2) ,则实数a的取值范围是 .
在(-1,+∞)上满足对任意x1<x2,都有f(x1)>f(x2) ,则实数a的取值范围是 .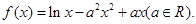
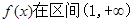 上是单调减函数,求实数a的取值范围;
上是单调减函数,求实数a的取值范围;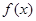 的极值;
的极值;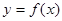 是定义在区间
是定义在区间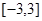 上的奇函数,且在
上的奇函数,且在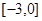 上单调递增,若
上单调递增,若 满足:
满足: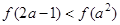 ,求
,求