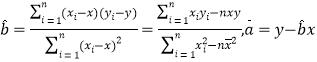题目内容
【题目】已知方程
的四个根组成一个首项为
的等差数列，则
_____．
【答案】
【解析】
把方程（x2﹣2x+m）（x2﹣2x+n）＝0化为x2﹣2x+m＝0，或x2﹣2x+n＝0，设
是第一个方程
的根，代入方程即可求得m，则方程的另一个根可求；设另一个方程的根为s，t，（s≤t）
根据韦达定理可知∴s+t＝2
根据等差中项的性质可知四个跟成的等差数列为，s，t，
，进而根据数列的第一项和第四项求得公差，则s和t可求，进而根据韦达定理求得n，最
后代入|m﹣n|即可．
方程（x2﹣2x+m）（x2﹣2x+n）＝0可化为
x2﹣2x+m＝0①，或x2﹣2x+n＝0②，
设是方程①的根，
则将代入方程①，可解得m
，
∴方程①的另一个根为．
设方程②的另一个根为s，t，（s≤t）
则由根与系数的关系知，s+t＝2，st＝n，
又方程①的两根之和也是2，
∴s+t
由等差数列中的项的性质可知，
此等差数列为，s，t，，
公差为[
]÷3
，
∴s
，t
，
∴n＝st
∴，|m﹣n|＝|
|．
故答案为：
练习册系列答案
一线名师权威作业本系列答案
相关题目
【题目】中央电视台播出的《朗读者》节目，受到广大人民群众的喜爱.随着节目的播出，极大激发了观众对朗读以及经典的阅读学习积累的热情，从中获准匪浅，现从观看节目的观众中随机统计了4位观众的周均阅读学习经典的知识的时间（单位：小时）与年龄（单位：岁），并制作了对照表（如下表所示）：
年龄 | 20 | 30 | 40 | 50 |
周均学习成语知识时间 | 2.5 | 3 | 4 | 4.5 |
由表中数据，试求线性回归方程
，并预测年龄为50岁观众周均学习阅读经典知识的时间.
参考公式：
