题目内容
【题目】已知某种细菌的适宜生长温度为10℃~25℃,为了研究该种细菌的繁殖数量![]() (单位:个)随温度
(单位:个)随温度![]() (单位:℃)变化的规律,收集数据如下:
(单位:℃)变化的规律,收集数据如下:
温度 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
繁殖数量 | 20 | 25 | 33 | 27 | 51 | 112 | 194 |
对数据进行初步处理后,得到了一些统计量的值,如下表所示:
|
|
|
|
|
|
|
18 | 66 | 3.8 | 112 | 4.3 | 1428 | 20.5 |
其中![]() ,
,![]() .
.
(1)请绘出![]() 关于
关于![]() 的散点图,并根据散点图判断
的散点图,并根据散点图判断![]() 与
与![]() 哪一个更适合作为该种细菌的繁殖数量
哪一个更适合作为该种细菌的繁殖数量![]() 关于温度
关于温度![]() 的回归方程类型(给出判断即可,不必说明理由);
的回归方程类型(给出判断即可,不必说明理由);
(2)根据(1)的判断结果及表格数据,建立![]() 关于
关于![]() 的回归方程(结果精确到0.1);
的回归方程(结果精确到0.1);
(3)当温度为25℃时,该种细菌的繁殖数量的预报值为多少?
参考公式:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二成估计分别为
的斜率和截距的最小二成估计分别为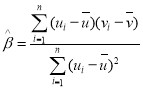 ,
,![]() .
.
参考数据:![]() .
.
【答案】(1) ![]() 更适合作为
更适合作为![]() 关于
关于![]() 的回归方程.(2)
的回归方程.(2) ![]() .(3)245.
.(3)245.
【解析】
(1)画出![]() 关于
关于![]() 的散点图,即可作出判定,得到结论.
的散点图,即可作出判定,得到结论.
(2)由(1)因为![]() ,得
,得![]() ,利用公式求得
,利用公式求得![]() 和
和![]() 的值,即可求得回归方程;
的值,即可求得回归方程;
(3)令![]() ,求得
,求得![]() ,即可得到结论.
,即可得到结论.
(1)由题意,![]() 关于
关于![]() 的散点图如下图所示.
的散点图如下图所示.
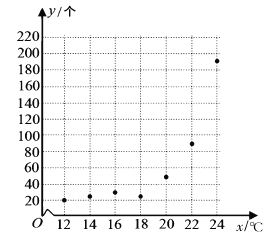
![]() 更适合作为
更适合作为![]() 关于
关于![]() 的回归方程.
的回归方程.
(2)由(1)因为![]() ,则
,则![]() ,
,
∴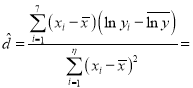
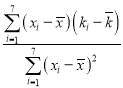
![]() ,
,
∴![]()
![]() ,
,
∴![]() 关于
关于![]() 的回归方程为
的回归方程为![]() .
.
(3)由(2)中的回归方程,令![]() ,求得
,求得![]() ,
,
所以当温度为![]() 时,预报值为
时,预报值为![]() .
.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目