题目内容
【题目】已知函数f(x)=![]() -ln(x+m).
-ln(x+m).
(1)设x=0是f(x)的极值点,求m,并讨论f(x)的单调性;
(2)当m≤2时,证明f(x)>0.
【答案】(1)![]() 在
在![]() 上是减函数;在
上是减函数;在![]() 上是增函数(2)见解析
上是增函数(2)见解析
【解析】
(1)![]() .
.
由x=0是f(x)的极值点得f '(0)=0,所以m=1.
于是f(x)=ex-ln(x+1),定义域为(-1,+∞),![]() .
.
函数![]() 在(-1,+∞)上单调递增,且f '(0)=0,因此当x∈(-1,0)时, f '(x)<0;当x∈(0,+∞)时, f '(x)>0.
在(-1,+∞)上单调递增,且f '(0)=0,因此当x∈(-1,0)时, f '(x)<0;当x∈(0,+∞)时, f '(x)>0.
所以f(x)在(-1,0)上单调递减,在(0,+∞)上单调递增.
(2)当m≤2,x∈(-m,+∞)时,ln(x+m)≤ln(x+2),故只需证明当m=2时, f(x)>0.
当m=2时,函数![]() 在(-2,+∞)上单调递增.
在(-2,+∞)上单调递增.
又f '(-1)<0, f '(0)>0,故f '(x)=0在(-2,+∞)上有唯一实根![]() ,且
,且![]() .
.
当![]() 时, f '(x)<0;当
时, f '(x)<0;当![]() 时, f '(x)>0,从而当
时, f '(x)>0,从而当![]() 时,f(x)取得最小值.
时,f(x)取得最小值.
由f '(x0)=0得![]() =
=![]() ,
,![]() ,
,
故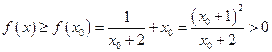 .
.
综上,当m≤2时, f(x)>0.

 学习实践园地系列答案
学习实践园地系列答案【题目】如图,已知抛物线![]() 经过
经过![]() ,
,![]() 两点,与
两点,与![]() 轴的另一个交点为
轴的另一个交点为![]() ,顶点为
,顶点为![]() ,连结
,连结![]() .
.
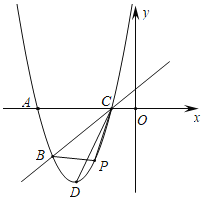
(1)求该抛物线的表达式;
(2)点![]() 为该抛物线上的一动点(与点
为该抛物线上的一动点(与点![]() 、
、![]() 不重合),设点
不重合),设点![]() 的横坐标为
的横坐标为![]() .当点
.当点![]() 在直线
在直线![]() 的下方运动时,求
的下方运动时,求![]() 的面积的最大值.
的面积的最大值.
【题目】某地随着经济的发展,居民收入逐年增长,下表是该地一建设银行连续五年的储蓄存款(年底余额),如下表1:
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
为了研究计算的方便,工作人员将上表的数据进行了处理, ![]() 得到下表2:
得到下表2:
时间代号t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
(Ⅰ)求z关于t的线性回归方程;
(Ⅱ)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程![]() ,其中
,其中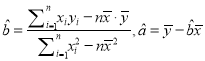 )
)
【题目】某小组为了研究昼夜温差对一种稻谷种子发芽情况的影响,他们分别记录了4月1日至4月5日的每天星夜温差与实验室每天每100颗种子的发芽数,得到如下资料:
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 |
温差 | 9 | 10 | 11 | 8 | 12 |
发芽数 | 38 | 30 | 24 | 41 | 17 |
利用散点图,可知![]() 线性相关。
线性相关。
(1)求出![]() 关于
关于![]() 的线性回归方程,若4月6日星夜温差
的线性回归方程,若4月6日星夜温差![]() ,请根据你求得的线性同归方程预测4月6日这一天实验室每100颗种子中发芽颗数;
,请根据你求得的线性同归方程预测4月6日这一天实验室每100颗种子中发芽颗数;
(2)若从4月1日![]() 4月5日的五组实验数据中选取2组数据,求这两组恰好是不相邻两天数据的概率.
4月5日的五组实验数据中选取2组数据,求这两组恰好是不相邻两天数据的概率.
(公式: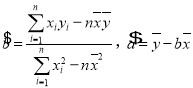 )
)