题目内容
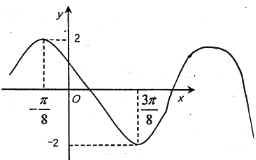
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的离心率为
的离心率为![]() ,直线
,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过原点的直线与椭圆![]() 交于
交于![]() 两点(
两点(![]() 不是椭圆
不是椭圆![]() 的顶点),点
的顶点),点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() ,直线
,直线![]() 与
与![]() 轴
轴![]() 轴分别交于
轴分别交于![]() 两点.
两点.
①设直线![]() 斜率分别为
斜率分别为![]() ,证明存在常数
,证明存在常数![]() 使得
使得![]() ,并求出
,并求出![]() 的值;
的值;
②求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() .
.
(2) ①证明见解析,![]() ;②
;②![]() .
.
【解析】试题分析:(1)首先由题意得到![]() ,即
,即![]() .
.
将![]() 代入
代入![]() 可得
可得![]() ,
,
由![]() ,可得
,可得![]() .
.![]() 得解.
得解.
(2)(ⅰ)注意从确定![]() 的表达式入手,探求使
的表达式入手,探求使![]() 成立的
成立的![]() .
.
设![]() ,则
,则![]() ,
,
得到![]() ,
,
根据直线BD的方程为![]() ,
,
令![]() ,得
,得![]() ,即
,即![]() .得到
.得到![]() .
.
由![]() ,作出结论.
,作出结论.
(ⅱ)直线BD的方程![]() ,
,
从确定![]() 的面积表达式
的面积表达式![]() 入手,应用基本不等式得解.
入手,应用基本不等式得解.
试题解析:(1)由题意知![]() ,可得
,可得![]() .
.
椭圆C的方程可化简为![]() .
.
将![]() 代入可得
代入可得![]() ,
,
因此![]() ,可得
,可得![]() .
.
因此![]() ,
,
所以椭圆C的方程为![]() .
.
(2)(ⅰ)设![]() ,则
,则![]() ,
,
因为直线AB的斜率![]() ,
,
又![]() ,所以直线AD的斜率
,所以直线AD的斜率![]() ,
,
设直线AD的方程为![]() ,
,
由题意知![]() ,
,
由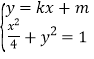 ,可得
,可得![]() .
.
所以![]() ,
,
因此![]() ,
,
由题意知,![]()
所以![]() ,
,
所以直线BD的方程为![]() ,
,
令![]() ,得
,得![]() ,即
,即![]() .
.
可得![]() .
.
所以![]() ,即
,即![]() .
.
因此存在常数![]() 使得结论成立.
使得结论成立.
(ⅱ)直线BD的方程![]() ,
,
令![]() ,得
,得![]() ,即
,即![]() ,
,
由(ⅰ)知![]() ,
,
可得![]() 的面积
的面积![]() ,
,
因为![]() ,当且仅当
,当且仅当![]() 时等号成立,
时等号成立,
此时S取得最大值![]() ,
,
所以![]() 的面积的最大值为
的面积的最大值为![]() .
.

【题目】2018年为我国改革开放40周年,某事业单位共有职工600人,其年龄与人数分布表如下:
年龄段 |
|
|
|
|
人数(单位:人) | 180 | 180 | 160 | 80 |
约定:此单位45岁~59岁为中年人,其余为青年人,现按照分层抽样抽取30人作为全市庆祝晚会的观众.
(1)抽出的青年观众与中年观众分别为多少人?
(2)若所抽取出的青年观众与中年观众中分别有12人和5人不热衷关心民生大事,其余人热衷关心民生大事.完成下列![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为年龄层与热衷关心民生大事有关?
的把握认为年龄层与热衷关心民生大事有关?
热衷关心民生大事 | 不热衷关心民生大事 | 总计 | |
青年 | 12 | ||
中年 | 5 | ||
总计 | 30 |
(3)若从热衷关心民生大事的青年观众(其中1人擅长歌舞,3人擅长乐器)中,随机抽取2人上表演节目,则抽出的2人能胜任才艺表演的概率是多少?
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
 .
.