题目内容
1.偶函数f(x)的定义域为R,若f(x+2)为奇函数,且f(1)=1,则f(9)+f(10)=( )| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
分析 根据函数的奇偶性的性质,得到f(x+8)=f(x),即可得到结论.
解答 解:∵f(x+2)为奇函数,
∴f(-x+2)=-f(x-2),
∵f(x)是偶函数,
∴f(-x+2)=f(x-2)=-f(x-2),
即f(x+4)=-f(x),
f(x+8)=f(x+4+4)=-f(x+4)=f(x),
则f(9)=f(1)=1,
f(10)=f(2),
当x=0时,由f(-x+2)=-f(x-2),
得f(2)=-f(-2)=-f(2),
即2f(2)=0,
则f(2)=0,
∴f(9)+f(10)=0+1=1,
故选:D.
点评 本题主要考查函数值的计算,利用函数奇偶性的性质,得到函数的对称轴是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.为了考察中学生的性别与是否喜欢数学课程之间的关系,在某校中学生中随机抽取了50名学生,得到如下列联表:
你认为性别与是否喜欢数学课程之间有关系的把握有( )
| 喜欢数学 | 不喜欢数学 | 合计 | |
| 男 | 13 | 10 | 23 |
| 女 | 7 | 20 | 27 |
| 合计 | 20 | 30 | 50 |
| A. | 0 | B. | 95% | C. | 99% | D. | 100% |
9. 电视传媒公司为了解某地区观众对某体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名,下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
电视传媒公司为了解某地区观众对某体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名,下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.
(1)根据已知条件完成下面的2×2列联表,并据此资料你是否认为“体育迷”与性别有关?
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
(2)将上述调查所得到的频率视为概率.现在从该地区大量电视观众中,采用随机抽样方法每次抽取1名观众,抽取3次,记被抽取的3名观众中的“体育迷”人数为X.若每次抽取的结果是相互独立的,求X的分布列,期望E(X)和方差D(X).
 电视传媒公司为了解某地区观众对某体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名,下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
电视传媒公司为了解某地区观众对某体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名,下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.
(1)根据已知条件完成下面的2×2列联表,并据此资料你是否认为“体育迷”与性别有关?
| 非体育迷 | 体育迷 | 合计 | |
| 男 | |||
| 女 | 10 | 55 | |
| 合计 |
| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
8.延迟退休年龄的问题,近期引发社会的关注. 人社部于2012年7月25日上午召开新闻发布会表示,我国延迟退休年龄将借鉴国外经验,拟对不同群体采取差别措施,并以“小步慢走”的方式实施.推迟退休年龄似乎是一种必然趋势,然而反对的声音也随之而起.现对某市工薪阶层关于“延迟退休年龄”的态度进行调查,随机抽取了50人,他们月收入的频数分布及对“延迟退休年龄”反对的人数
根据已知条件完成下面的2×2列联表,问能否在犯错误的概率不超过0.01的前提下认为月收入以5000为分界点的“延迟退休年龄”的态度有差异?
附:临界值表
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| 月收入(元) | [1000,2000) | [2000,3000) | [3000,4000) | [4000,5000) | [5000,6000) | [6000,7000) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 反对人数 | 4 | 8 | 12 | 5 | 2 | 1 |
| 月收入不低于5000元的人数 | 月收入低于5000元的人数 | 总计 | |
| 反对 | |||
| 赞成 | |||
| 总计 |
| P(k2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 |
 .
.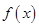 最小正周期;
最小正周期;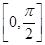 上的最大值和最小值.
上的最大值和最小值.