题目内容
已知函数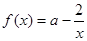 。
。
(1)讨论 的奇偶性;
的奇偶性;
(2)判断 在
在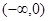 上的单调性并用定义证明。
上的单调性并用定义证明。
(1)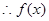 不具备奇偶性
不具备奇偶性
(2)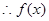 在
在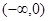 上单调递增
上单调递增
解析试题分析:解:(1)函数 的定义域为
的定义域为 关于原点对称。 1分
关于原点对称。 1分
(1)方法1: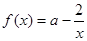 ,
,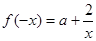 2分
2分
若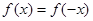 ,则
,则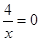 ,无解,
,无解,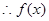 不是偶函数 4分
不是偶函数 4分
若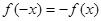 ,则
,则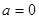 ,显然
,显然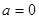 时,
时, 为奇函数
为奇函数
综上,当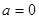 时,
时, 为奇函数;当
为奇函数;当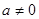 时,
时, 不具备奇偶性 6分
不具备奇偶性 6分
方法2:函数 的定义域为
的定义域为 关于原点对称。 1分
关于原点对称。 1分
当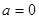 时,
时,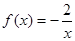 ,
,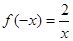 ,
,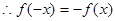 ,
,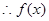 为奇函数: 4分
为奇函数: 4分
当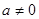 时,
时,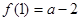 ,
,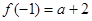 ,显然
,显然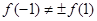
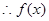 不具备奇偶性。 6分
不具备奇偶性。 6分
(2)函数 在
在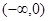 上单调递增; 7分
上单调递增; 7分
证明:任取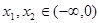 且
且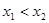 ,则
,则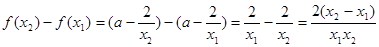 9分
9分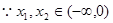 且
且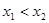 ,
,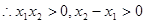 ,
,
从而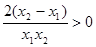 ,故
,故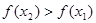 , 11分
, 11分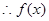 在
在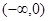 上单调递增。 12分
上单调递增。 12分
考点:函数的奇偶性和单调性
点评:解决的关键是对于函数奇偶性和单调性概念的准确判定和运用,属于基础题。

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
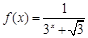 ,(1)分别求
,(1)分别求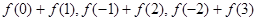 ;(2)然后归纳猜想一般性结论,并给出证明.
;(2)然后归纳猜想一般性结论,并给出证明. 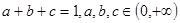 ,求证:
,求证: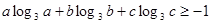 ;
;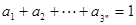 ,
,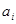 >0(i=1,2,3,…,3n),求证:
>0(i=1,2,3,…,3n),求证: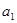
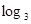
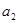
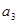
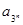
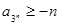
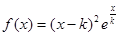 .
. 的单调区间;
的单调区间;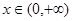 ,有
,有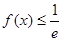 恒成立,求
恒成立,求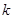 的取值范围.
的取值范围. .
.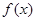 为定义域上的单调函数,求实数m的取值范围;
为定义域上的单调函数,求实数m的取值范围;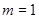 ,
,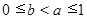 时,证明:
时,证明: .
. .
.
 是偶函数;
是偶函数;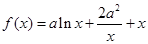 .
.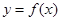 在点
在点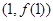 处的切线与直线
处的切线与直线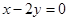 垂直,求实数
垂直,求实数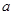 的值.
的值.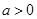 ,求
,求 的最小值
的最小值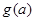 ;
;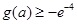 .
.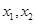 是函数
是函数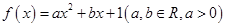 的两个零点,函数
的两个零点,函数 的最小值为
的最小值为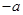 ,记
,记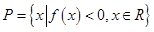
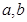 );
); 在什么范围内,函数
在什么范围内,函数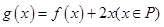 存在最小值?
存在最小值?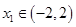 ,试确定
,试确定 的取值范围。
的取值范围。 在
在 上是偶函数,其图象关于直线
上是偶函数,其图象关于直线 对称,且在区间
对称,且在区间 上是单调函数,求
上是单调函数,求 和
和 的值.
的值.