题目内容
已知函数 .
.
(1)若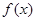 为定义域上的单调函数,求实数m的取值范围;
为定义域上的单调函数,求实数m的取值范围;
(2)当m=-1时,求函数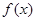 的最大值;
的最大值;
(3)当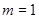 ,
,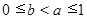 时,证明:
时,证明: .
.
(1)m≥0(2)0(3)构造函数利用导数证明
解析试题分析:(1)由已知得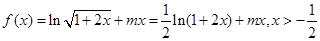 ,
,
所以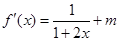 2分
2分
若f(x)在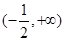 上是增函数,则
上是增函数,则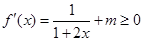 ,即
,即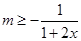 在
在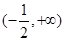 恒成立,
恒成立,
而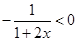 ,故m≥0; 4分
,故m≥0; 4分
若f(x)在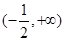 上是减函数,则
上是减函数,则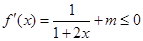 ,即
,即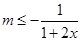 在
在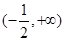 恒成立,
恒成立,
而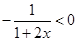 ,故这样的m不存在. 5分
,故这样的m不存在. 5分
经检验,当m≥0时, 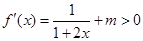 对
对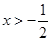 恒成立,
恒成立,
∴当m≥0时,f(x)在定义域上是单调增函数. 6分
(2)当m =-1时, 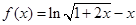 ,则
,则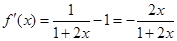 7分
7分
当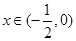 时,
时,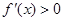 ,此时f(x)为增函数,
,此时f(x)为增函数,
当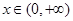 时,
时, 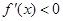 ,此时f(x)为减函数 9分
,此时f(x)为减函数 9分
∴f(x)在x = 0时取得最大值,最大值为0. 10分
(3)当m = 1时,令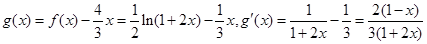 , 11分
, 11分
在[0,1]上总有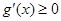 ,即
,即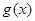 在[0,1]上递增 , 12分
在[0,1]上递增 , 12分
∴当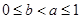 时,
时, ,即
,即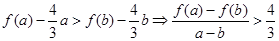 , 13分
, 13分
令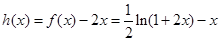 ,由(2)知它在[0,1]上递减,
,由(2)知它在[0,1]上递减,
所以当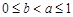 时,
时,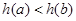 ,即
,即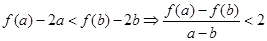 , 14分
, 14分
综上所述,当m = 1,且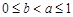 时,
时, . 15分
. 15分
考点:本小题主要考查利用导数研究函数的单调性、极值、最值等和构造函数证明不等式.
点评:导数是研究函数性质的有力工具,利用导数研究函数性质时,不要漏掉函数的定义域,求函数的极值、最值等时最好列表格说明,证明不等式一般要构造函数利用单调性证明问题.

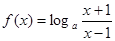
 .
. 的奇偶性;
的奇偶性; 上的单调性,并给出证明;
上的单调性,并给出证明;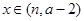 时,函数
时,函数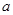 与
与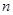 的值;
的值; ,函数
,函数
 的极小值;
的极小值; 在
在 上为单调增函数,求
上为单调增函数,求 的取值范围;
的取值范围; ,若在
,若在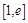 (
( 是自然对数的底数)上至少存在一个
是自然对数的底数)上至少存在一个 ,使得
,使得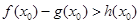 成立,求
成立,求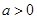 ,函数
,函数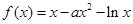 .
.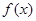 是单调函数,求实数
是单调函数,求实数 的取值范围;
的取值范围;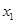 、
、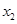 ,证明:
,证明: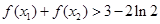 .
.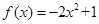 是偶函数,且在
是偶函数,且在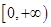 上是减少的。(13分)
上是减少的。(13分)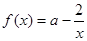 。
。 的奇偶性;
的奇偶性;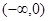 上的单调性并用定义证明。
上的单调性并用定义证明。 (a>0,且a≠1),
(a>0,且a≠1), =
= .
. 的图象恒过定点A,求A点坐标;
的图象恒过定点A,求A点坐标; 的图像过点(2,
的图像过点(2, ),证明:函数
),证明:函数 在
在 (1,2)上有唯一的零点.
(1,2)上有唯一的零点. 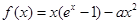
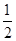 ,求f(x)的单调区间;
,求f(x)的单调区间;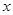 ≥0时f(x)≥0,求a的取值范围。
≥0时f(x)≥0,求a的取值范围。
 ,且
,且 能表示成一个奇函数
能表示成一个奇函数 和一个偶函数
和一个偶函数 的和.
的和. :函数
:函数 上是增函数;命题
上是增函数;命题 :函数
:函数 的取值范围.
的取值范围. 和
和 的大小.
的大小.