题目内容
已知动点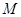
到
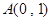的距离比它到
轴的距离多一个单位．
（Ⅰ）求动点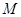的轨迹
的方程；
（Ⅱ）过点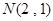
作曲线的切线
，求切线的方程，并求出与曲线及
轴所围成图形的面积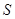
．
（Ⅰ）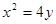
（Ⅱ）切线的方程为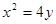：，所求的图形的面积为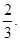
解析试题分析：（Ⅰ）设动点M的坐标为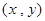
，
依题意得：动点M到点
的距离与它到直线
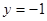的距离相等，
由抛物线定义知：M的轨迹C是以为焦点，直线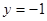为准线的抛物线，
其方程为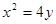：． ……6分
（Ⅱ）∵曲线C的方程可写成：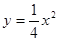
，
注意到点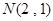在曲线C上，过点N的切线斜率为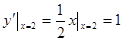
，
故所求的切线的方程为：
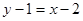即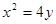． ……9分
由定积分的几何意义，所求的图形的面积
． ……13分
考点：本小题注意考查抛物线标准方程的求解，导数的运算，切线的求解和定积分的计算.
点评：解决轨迹方程问题时，经常先根据定义求出曲线类型再求解，因此圆、椭圆、双曲线、抛物线的定义尤其重要，要熟练掌握，灵活应用.
练习册系列答案
相关题目
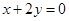与圆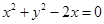
的交点为A、B，
的焦点与双曲线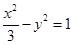
的右焦点重合.
，
是抛物线
上相异两点，且满足
．
的中垂线经过点
，求直线
轴于点
，求
的面积的最大值及此时直线
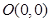的距离是到定点
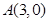距离的二倍，求这条曲线的方程．
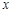轴上，长轴长是短轴长的2倍的椭圆经过点M(2,1) 
平行于
，且与椭圆交于A、B两个不同点.
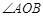为钝角，求直线
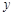轴上的截距m的取值范围；
、
分别是椭圆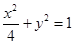
的左、右焦点。
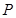是第一象限内该椭圆上的一点，
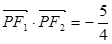，求点P的坐标；
与椭圆交于不同的两点A、B，且
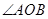为锐角（其中
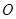为坐标原点），求直线
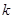的取值范围。
的顶点在坐标原点，它的准线经过双曲线
：
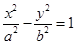的一个焦点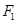
且垂直于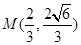
．
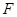的坐标；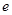
．
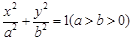的离心率为
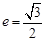，且过点（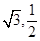
），
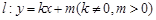与椭圆交于P，Q两点，且以PQ为对角线的菱形的一顶点为（-1，0），求：△OPQ面积的最大值及此时直线的方程.