题目内容
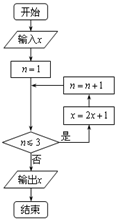 (2013•东莞二模)已知实数,x∈[0,10],执行如图所示的程序框图,则输出的x不小于47的概率为
(2013•东莞二模)已知实数,x∈[0,10],执行如图所示的程序框图,则输出的x不小于47的概率为| 1 |
| 2 |
| 1 |
| 2 |
分析:由程序框图的流程,写出前三项循环得到的结果,得到输出的值与输入的值的关系,令输出值大于等于47得到输入值的范围,利用几何概型的概率公式求出输出的x不小于47的概率.
解答:解:设实数x∈[0,10],
经过第一次循环得到x=2x+1,n=2
经过第二循环得到x=2(2x+1)+1,n=3
经过第三次循环得到x=2[2(2x+1)+1]+1,n=3此时输出x
输出的值为8x+7
令8x+7≥47得x≥5
由几何概型得到输出的x不小于47的概率为P=
=
故答案为:
.
经过第一次循环得到x=2x+1,n=2
经过第二循环得到x=2(2x+1)+1,n=3
经过第三次循环得到x=2[2(2x+1)+1]+1,n=3此时输出x
输出的值为8x+7
令8x+7≥47得x≥5
由几何概型得到输出的x不小于47的概率为P=
| 10-5 |
| 10 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:解决程序框图中的循环结构时,一般采用先根据框图的流程写出前几次循环的结果,根据结果找规律.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
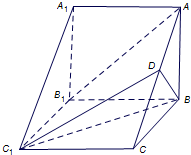 (2013•东莞二模)如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.
(2013•东莞二模)如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.