题目内容
(2013•东莞二模)设Sn为数列{an}前n项和,对任意的n∈N*,都有Sn=2-an,数列{bn}满足bn=
,b1=2a1,
(1)求证:数列{an}是等比数列,并求{an}的通项公式;
(2)求数列{bn}的通项公式;
(3)求数列{
}的前n项和Tn.
| bn-1 |
| 1+bn-1 |
(1)求证:数列{an}是等比数列,并求{an}的通项公式;
(2)求数列{bn}的通项公式;
(3)求数列{
| 1 |
| an+2bn |
分析:(1)当n=1时,由a1=S1=2-a1,可求a1,n≥2时,由an=Sn-Sn-1,可得an=与an-1之间的递推关系,结合等比数列的通项公式可求an
(2)由bn=
,可得
-
=1(n≥2),结合等差数列的通项公式可求
,进而可求bn
(3)由(1)(2)可求
,利用错位相减求和即可求解
(2)由bn=
| bn-1 |
| 1+bn-1 |
| 1 |
| bn |
| 1 |
| bn-1 |
| 1 |
| bn |
(3)由(1)(2)可求
| 1 |
| an+2bn |
解答:(本小题满分14分)
证明:(1)当n=1时,a1=S1=2-a1,解得a1=1. …(1分)
当n≥2时,an=Sn-Sn-1=an-1-an,即2an=an-1.
∴
=
(n≥2). …(2分)
∴数列{an}是首项为1,公比为
的等比数列,即an=(
)n-1,n∈N*. …(4分)
解:(2)b1=2a1=2. …(5分)
∵bn=
,
∴
=
+1,即
-
=1(n≥2). …(6分)
∴{
}是首项为
,公差为1的等差数列. …(7分)
∴
=
+(n-1)•1=
,bn=
…(8分)
(3)∵an+2=(
)n+1,bn=
则
=2n(2n-1). …(9分)
所以Tn=
+
+
+…+
+
,…(10分)
即Tn=21×1+22×3+23×5+…+2n-1×(2n-3)+2n×(2n-1),①…(11分)
则2Tn=22×1+23×3+24×5+…+2n×(2n-3)+2n+1×(2n-1),②…(12分)
②-①得Tn=2n+1×(2n-1)-2-23-24-…-2n+1,…(13分)
故Tn=2n+1×(2n-1)-2-
=2n+1×(2n-3)+6. …(14分)
证明:(1)当n=1时,a1=S1=2-a1,解得a1=1. …(1分)
当n≥2时,an=Sn-Sn-1=an-1-an,即2an=an-1.
∴
| an |
| an-1 |
| 1 |
| 2 |
∴数列{an}是首项为1,公比为
| 1 |
| 2 |
| 1 |
| 2 |
解:(2)b1=2a1=2. …(5分)
∵bn=
| bn-1 |
| 1+bn-1 |
∴
| 1 |
| bn |
| 1 |
| bn-1 |
| 1 |
| bn |
| 1 |
| bn-1 |
∴{
| 1 |
| bn |
| 1 |
| 2 |
∴
| 1 |
| bn |
| 1 |
| 2 |
| 2n-1 |
| 2 |
| 2 |
| 2n-1 |
(3)∵an+2=(
| 1 |
| 2 |
| 2 |
| 2n-1 |
则
| 1 |
| an+2bn |
所以Tn=
| 22 |
| b1 |
| 23 |
| b2 |
| 24 |
| b3 |
| 2n |
| bn-1 |
| 2n+1 |
| bn |
即Tn=21×1+22×3+23×5+…+2n-1×(2n-3)+2n×(2n-1),①…(11分)
则2Tn=22×1+23×3+24×5+…+2n×(2n-3)+2n+1×(2n-1),②…(12分)
②-①得Tn=2n+1×(2n-1)-2-23-24-…-2n+1,…(13分)
故Tn=2n+1×(2n-1)-2-
| 23(1-2n-1) |
| 1-2 |
点评:本题主要考查了利用数列的递推公式求解数列的通项公式、等差数列与等比数列的通项公式的应用,还考查了错位相减求和方法的应用

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
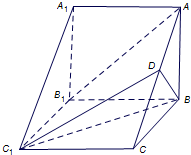 (2013•东莞二模)如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.
(2013•东莞二模)如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.