已知集合A={x|x2-2ax-8a2＞0}(1)当a=1时.求集合∁RA,⊆∁RA.求实数a的取值范围．题目和参考答案——青夏教育精英家教网——

题目内容

14．已知集合A={x|x²-2ax-8a²＞0}
（1）当a=1时，求集合∁_RA；
（2）若a＞0，且（-1，1）⊆∁_RA，求实数a的取值范围．

分析（1）把a的值代入A中求出解集确定出A，进而求出A的补集；
（2）由a大于0，表示出A中不等式的解集，确定出A的补集，根据区间（-1，1）为A补集的子集，求出a的范围即可．

解答解：（1）把a=1代入A中不等式得：x²-2x-8＞0，即（x-4）（x+2）＞0，
解得：x＜-2或x＞4，即A=（-∞，-2）∪（4，+∞），
则∁_RA=[-2，4]；
（2）∵a＞0，
∴不等式x²-2ax-8a²≤0的解为：-2a≤x≤4a，
∵（-1，1）⊆∁_RA，
∴ $\left\{\begin{array}{l}{a＞0}\\{-2a≤-1}\\{4a≥1}\end{array}\right.$ ，
解得：a≥ $\frac{1}{2}$ ，
则实数a的取值范围为[ $\frac{1}{2}$ ，+∞）．

点评此题考查了补集及其运算，熟练掌握补集的定义是解本题的关键．

练习册系列答案

名校课堂系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

4．设AB是椭圆

\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1

$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ （a＞b＞0）中不平行于对称轴且过原点的一条弦，M是椭圆上一点，直线AM与BM的斜率之积k_AM•k_BM=

- \frac{16}{25}

$-\frac{16}{25}$ ，则该椭圆的离心率为

\frac{3}{5}

$\frac{3}{5}$ ．

5．设函数f（x）=|2x+1|+|2x-a|+a，x∈R．
（Ⅰ）当a=3时，求不等式f（x）＞7的解集；
（Ⅱ）对任意x∈R恒有f（x）≥3，求实数a的取值范围．

2．在x轴上有一点P（4，0），在圆x²+y²=4上任取一点Q，求线段PQ的中点轨迹方程．

9．有5位学生和2位老师并坐一排合影，若教师不能坐在两端，且要坐在一起，则有多少种不同坐法（　　）

19．已知函数f（x）=x²-2ax-2alnx（a∈R），则下列说法正确的是①③④．
①当a＜0时，函数y=f（x）有零点；
②若函数y=f（x）有零点，则a＜0；
③存在a＞0，函数y=f（x）有唯一的零点；
④若函数y=f（x）有唯一的零点，则a≤1．

6．某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作了四次试验，得到的数据如下：

零件的个数x（个）	2	3	4	5
加工的时间y（小时）	2.5	3	4	4.5

y关于x的线性回归方程

ˆ y

$\widehat{y}$ =

ˆ a x + ˆ b

$\widehat{a}x+\widehat{b}$ 为

^y

$\hat{y}$ =0.7x+1.05．

3．如图，已知向量

\to a

$\overrightarrow{a}$ ，

\to b

$\overrightarrow{b}$ ，

\to c

$\overrightarrow{c}$ 不共线，求作向量

\to a

$\overrightarrow{a}$ +

\to b

$\overrightarrow{b}$ +

\to c

$\overrightarrow{c}$ ．

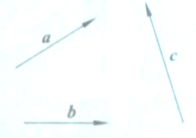
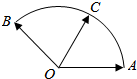给定两个长度为1的平面向量

- - \to O A

$\overrightarrow{OA}$ 和

- - \to O B

$\overrightarrow{OB}$ ，它们的夹角为120°如图所示，点C在以O为圆心的圆弧

- - \to A B

$\overrightarrow{AB}$ 上变动．若

- - \to O C

$\overrightarrow{OC}$ =x

- - \to O A

$\overrightarrow{OA}$ +y

- - \to O B

$\overrightarrow{OB}$ ，其中x，y∈R，则x+y的最大值是（　　）

\sqrt{2}

$\sqrt{2}$

\sqrt{3}

$\sqrt{3}$