题目内容
【题目】已知向量 
=（﹣2，4）， 
=（﹣1，﹣2）．
（1）求 ， 的夹角的余弦值；
（2）若向量 ﹣λ 与2 + 垂直，求λ的值．
【答案】
（1）解：向量 
=（﹣2，4）， 
=（﹣1，﹣2），
∴ =﹣2×（﹣1）+4×（﹣2）=﹣6，
| |= 
=2 
，
| |= 
= ；
∴ ， 夹角的余弦值为
cosθ= 
= 
=﹣ 
；
（2）解：∵ ﹣λ =（﹣2，4）﹣（﹣λ，﹣2λ）=（λ﹣2，2λ+4），
2 + =（﹣4，8）+（﹣1，﹣2）=（﹣5，6）；
又向量 ﹣λ 与2 + 垂直，
∴（ ﹣2λ ）（2 + ）=﹣5（λ﹣2）+6（2λ+4）=0，
解得λ=﹣ 
．
【解析】（1）根据平面向量的数量积与夹角公式，即可求出两向量夹角的余弦值；（2）根据平面向量的坐标运算与两向量垂直，数量积为0，列出方程求出λ的值．
【考点精析】认真审题，首先需要了解数量积表示两个向量的夹角(设
、
都是非零向量，
，
，
是与
的夹角，则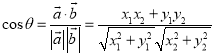
)．
练习册系列答案
相关题目
【题目】如图，四棱锥P﹣ABCD中，PD⊥底面ABCD，AB∥DC，AD⊥DC，AB=AD=1，DC=2，PD 
，M为棱PB的中点． （Ⅰ）证明：DM⊥平面PBC；
（Ⅱ）求二面角A﹣DM﹣C的余弦值．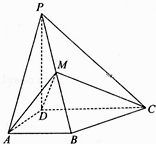
【题目】某市家庭煤气的使用量x（m3）和煤气费f（x）（元） 满足关系f（x）= 
，已知某家庭今年前三个月的煤气费如表：
月份 | 用气量 | 煤气费 |
一月份 | 4m3 | 4 元 |
二月份 | 25m3 | 14 元 |
三月份 | 35m3 | 19 元 |
若四月份该家庭使用了20m3的煤气，则其煤气费为（ ）元．
A.10.5
B.10
C.11.5
D.11